Напряжения и деформации: Напряжения и деформации в металлах — Студопедия

Деформации и напряжения — Студопедия

Напряжение – мера внутренних сил, возникающих в материале под влиянием внешних воздействий (нагрузок, изменения температуры и пр.). Для изучения напряжений через произвольную точку тела мысленно проводится сечение (рис. 3.1) и отбрасывается одна из половин тела. Действие отброшенной половины на другую половину заменяют внутренними силами.

Рис. 3.1. Схема замены внешних сил на внутренние напряжения

В малом элементе сечения площадью dS в окрестности произвольной точки А действует произвольно направленная внутренняя сила dF.
Отношение р = dF/dS называется вектором напряжения в точке А по площадке dS. Составляющие вектора напряжения, действующие по нормали к площадке, обозначаются σ и называются нормальными напряжениями, а действующие вдоль площадки называются касательными напряжениями τ в точке А по площадке dS, причём σ² + τ² = р².

В общем случае напряженное состояние тела в точке А характеризуется совокупностью всех векторов напряжений для всевозможных сечений (площадок, проходящих через точку А), а значит и для любого направления. Напряженное состояние в точке А может быть определено с помощью тензора напряжений и характеризуется девятью компонентами по трем осям координат (три нормальных и шесть касательных). Касательные напряжения попарно равны (τ_ху = τ_ух, τ_хz = τ_zх, τ_уz = τ_zу), т. е. остается всего шесть компонентов. Напряжения выражаются в Па (паскалях).

Т_н

= . (3.1)

Для тензора характерным является закон, по которому преобразуется его компоненты при повороте осей координат. При повороте системы координат можно отыскать такое ее положение, когда касательные напряжения будут равны нулю. Эти направления называют главными.

Главные направления тензора напряжений определяются условием, зависящим от трех инвариантов I₁, I₂, I₃ .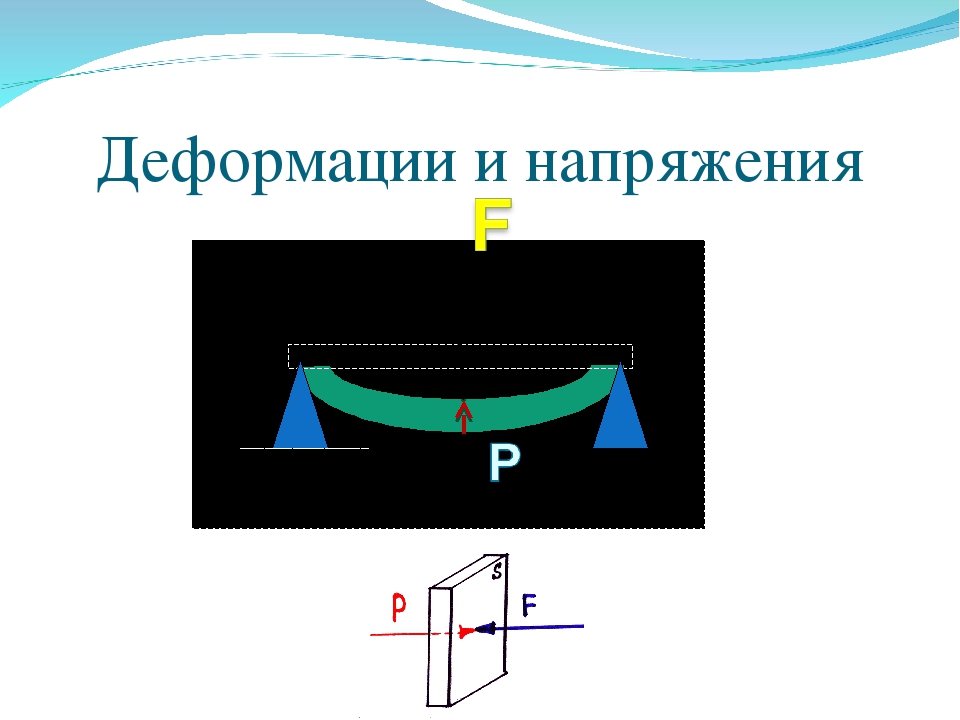

Первым инвариантом I₁ тензора напряжений является сумма нормальных напряжений:

I₁ = σ_х + σ_у + σ_z = 3σ

0. (3.2)

Среднее значение трёх нормальных напряжений называют гидростатическим давлением:

σ₀ = (σ_х + σ_у + σ_z)/3. (3.3)

Гидростатическому давлению соответствует тензор напряжений, нормальные компоненты которого равны σ₀, а касательные – нулю. Поскольку гидростатическое давление не вызывает в металле пластических деформаций, его исключают из системы напряжений. Оставшуюся часть тензора называют девиатором напряжений S_σ:

(3.4)

Второй инвариант I₂ тензора напряжений определяется следующим выражением:

I₂ = σ_х σ_у + σ_х σ_z + σ_уσ_z – τ²_ху – τ²_уz – τ²_zх. (3.5)

Величины, пропорциональные корню квадратному из второго инварианта девиатора напряжений, называют интенсивностью касательных напряжений τ_i и интенсивностью нормальных напряжений σ_i:

, . (3.6)

Напряжения в материале могут возникнуть при физико-химических процессах, при неравномерном распределении температуры (при нагреве и охлаждении металла), а также вследствие фазовых превращений при термической обработке. При этом напряжения, возникающие в объеме всего тела, называют

макронапряжениями (или напряжениями Ι рода), а напряжения, возникающие в объеме одного зерна, называют микронапряжениями (или напряжениями ΙΙ рода). Напряжения, возникающие в объемах порядка нескольких параметров кристаллической решетки, называются субмикроскопическими (или напряжениями ΙΙΙ рода). Деформациями называют изменения формы или размеров тела (или части тела) под действием внешних сил, а также при нагревании или охлаждении и других воздействиях, вызывающих изменение относительного положения частиц тела (рис. 3.2).

Рис. 3.2. Схема деформации: а) линейная деформация, б) угловая деформация

С геометрической точки зрения деформированное состояние в точке описывается тензором деформации:

(3.7)

Компоненты , характеризуют линейные деформации волокон, расположенных по осям x, y, z: относительные удлинения (или относительные укорочения), а компоненты – углы поворота двух взаимно перпендикулярных до деформации волокон (или деформации сдвига).

Для компонент деформаций сдвига справедливы равенства:

, , . (3.8)

При повороте системы координат все компоненты тензора деформации преобразуются по определенным линейным относительно направляющих косинусов соотношениям. В теории деформации и линейных преобразований доказывается, что из всех возможных направлений осей координат существует тройка взаимно перпендикулярных направлений (главных направлений), относительно которых все сдвиговые компоненты деформации равны нулю. Главные направления деформаций определяются тремя скалярными величинами, не зависящими от положения системы координат и поэтому называемыми инвариантами.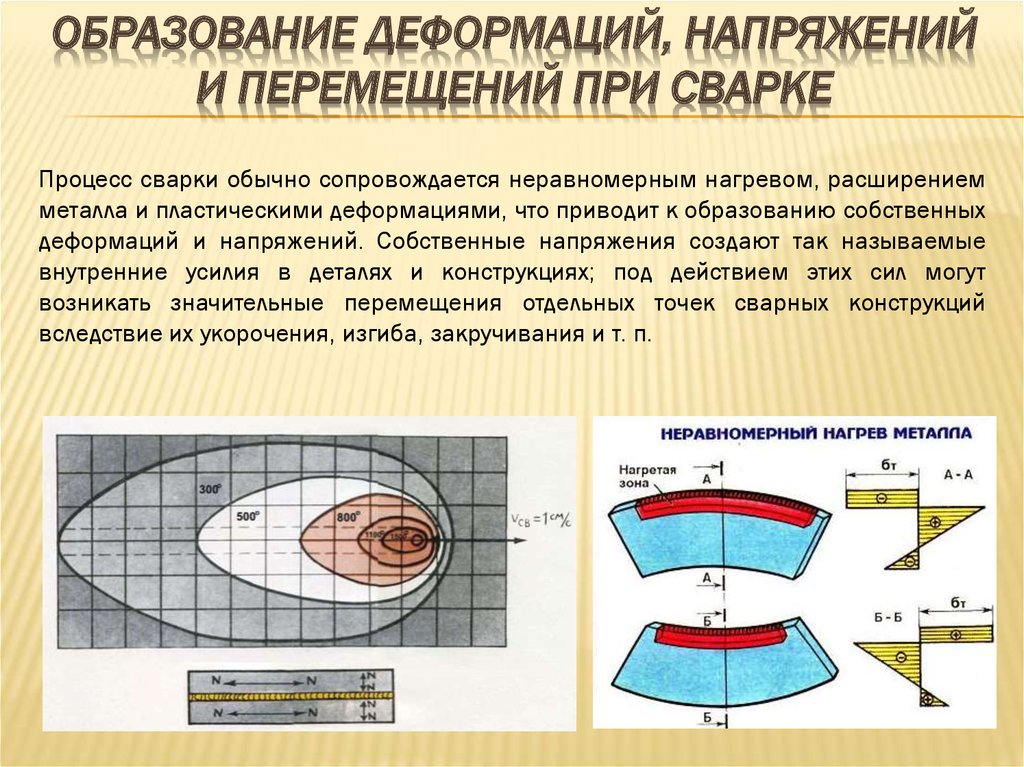

Первый инвариант используется для записи условия постоянства объема деформируемого металла:

= 0. (3.9)

Второй инвариант тензора деформации имеет вид:

I₂ = . (3.10)

Величина, пропорциональная корню квадратному из второго инварианта, называется

интенсивностью деформаций и используется для характеристики деформаций в общем случае деформированного состояния.

. (3.11)

Простейшие схемы деформирования – растяжение, сжатие, сдвиг, кручение, изгиб. Первые две схемы (растяжение и сжатие) могут быть описаны только линейными компонентами, вторые (сдвиг, кручение, изгиб) – только сдвиговыми (угловыми).

Напряжение и деформация

Физика > Напряжение и деформация

Отношение силы к площади именуют напряжением, а отношение перемены длины к длине  – деформацией.

Задача обучения

• Понять, как силы влияют на форму объекта.

Основные пункты

• Отношение силы к площади называют напряжением, а отношение перемены длины к длине  – деформацией.
• Напряжение и деформация связаны модулем Юнга (постоянная), меняющимся в зависимости от материала. Это выражается в формуле: напряжение = Y ⋅ деформацию.
• Материал с высоким модулем упругости обладает высокой прочностью в растяжении. Они очень устойчивые и требуют большой силы для деформирования огромного количества.

Термины

• Деформация – изменение материала под действием напряжения или силы отношения деформации к исходному размеру материала – инженерное напряжение (ϵ). Деформация определяется как естественный логарифм соотношения финальной размерности к изначальной.
• Напряжение – внутреннее распределение силы на единицу площади внутри тела, реагирующего на приложенные силы, которые приводят к деформации (σ).

Сейчас мы рассмотрим силы, влияющие на движение объекта и форму. Если бульдозер вдавливает машину в стену, то транспорт не пройдет сквозь нее, а изменить свою форму. Это случается из-за присутствия силы деформации. Все знают, что даже незначительные силы вызывают неприметные деформации. При малых видно два момента: объект возвращает изначальную форму, когда сила перестает действовать и размер деформации пропорционален силе. Здесь наблюдается закон Гука: F = k ⋅ ΔL, где ΔL – изменение длины, а k – постоянная, зависящая от свойств материала.

Давайте рассмотрим виды деформации: изменение длины (растяжение и сжатие), боковой сдвиг (напряжение) и изменение объема. Ниже представлена диаграмма напряжения и деформации.

Напряжение: стержень растягивается на длину ΔL, когда сила воздействует параллельно длине. (b) Сжатие: тот же стержень сжимается силами с одинаковой величиной в противоположном направлении. При малых деформациях и однородных материалах ΔL остается практически одинаковой. В случае с большими деформациями площадь поперечного сечения меняется

Отношение силы к площади именуют напряжением, а отношение перемены длины к длине – деформацией. Напряжение и деформация связаны модулем Юнга (постоянная), изменяющимся в зависимости от материала.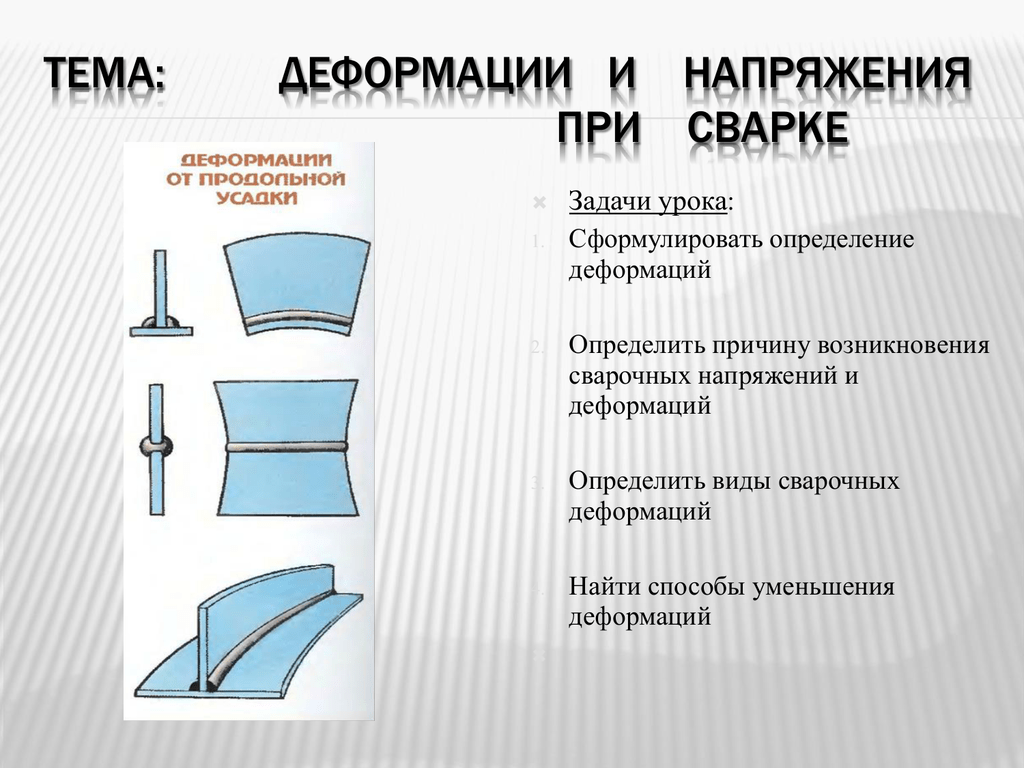 Модуль Юнга выражается в формуле: напряжение = Y ⋅ деформацию. Материал с высоким модулем упругости обладает высокой прочностью в растяжении. Они очень устойчивые и требуют большой силы для деформирования огромного количества.

---

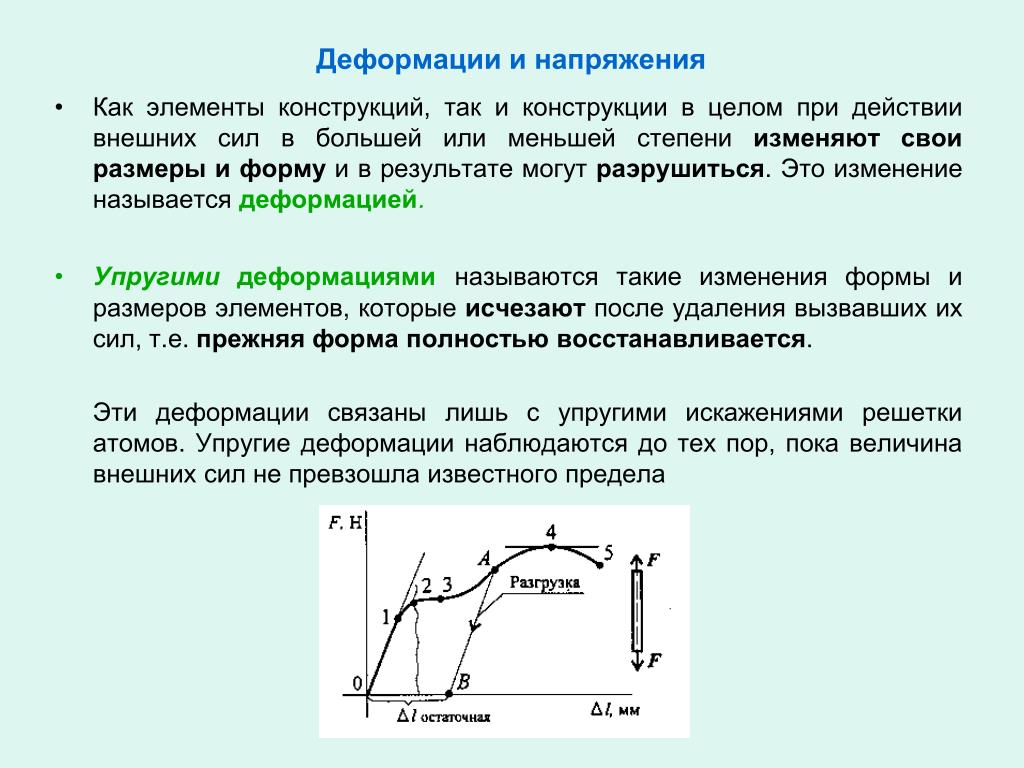
2.2. Деформации и напряжения

быть выражено через коэффициент поперечной деформации, называемый также коэффициентом Пуассона μ:

μ = ε1/ ε.

Коэффициент Пуассона так же, как и модули упругости, является характеристикой упругих свойств материала. Все три константы упругости материала связаны между собой следующей зависимостью:

G = Е/2(1 + μ).

Наибольшее напряжение, при снятии которого остаточные деформации не превышают некоторой заданной малой величины(обычно менее

0,2 %), называют пределом упругости sУПР.

Если за участком пропорциональности напряжения и деформации следует площадка текучести, соответствующая увеличению деформации при постоянном напряжении (рис. 3.9), то это напряжение называют пределом текучести sТ. При отсутствии таковой площадки пределом текуче-

сти считают напряжение, соответствующее некоторому установленному небольшому уровню деформации (например, 0,2 %) – s0,2.

Область справедливости закона Гука устанавливаетсяпределом пропорциональности sПЦ. Поскольку пропорциональность напряжения -де формации обычно выполняется во всей области упругости, при практических расчетах предел пропорциональности принимают равным пределу упругости (или меньше).

Для использования диаграмм растяжения при других, более сложных схемах деформирования напряжениеs z заменяют интенсивностью напряжений si , а деформацию ez – интенсивностью деформаций ei .

Пластичность характеризуется относительным удлинением и относительным сужением. Относительное удлинение δ – это относительное приращение (lK – l0) расчетной длины образца после разрыва к его первоначальной расчетной длине l0, выраженное в процентах:

d = [(lK — l0 )/ l0 ]×100 %.

Относительное сужение ψ – это соотношение разности начальной и конечной площади (S0 – SK) поперечного сечения образца после разрыва к начальной площади S0 поперечного сечения, выраженное в процентах:

y = [(S0 — SK )/ S0 ]×100 %.

Испытания на растяжение не всегда оценивают склонность материала к хрупкому разрушению, поэтому применяют испытания для определения ударной вязкости, отличающиеся от обычных испытаний на растяжение тем, что образец испытывается на изгиб при ударном(динамическом) нагружении.

Ударная вязкость – способность материала сопротивляться динамическим нагрузкам, определяется как отношение затраченной на излом ра-

15.Напряжения. Виды напряжения, виды деформации. Правила знаков. Примеры расчета плоского напряженного состояния.

Напряжением называется интенсивность действия внутренних сил в точке тела, то есть, напряжение — это внутреннее усилие, приходящееся на единицу площади. По своей природе напряжение — это поверхностная нагрузка, возникающая на внутренних поверхностях соприкасания частей тела.

 Деформацией называется изменение размеров и формы тела под действием приложенных сил.

Напряжением называется отношение действующего усилия к площади поперечного сечения тела или образца σ = P/F.     В зависимости от направления действия силы нормальные напряжения подразделяют на растягивающие и сжимающие. Различают временные и остаточные напряжения.     Временные напряжения возникают под действием внешней нагрузки и исчезают после ее снятия, остаточные — остаются в теле после прекращения действия нагрузки.

Если после прекращения действия внешних сил изменения формы, структуры и свойств тела полностью устраняются, то такая деформация называется упругой.

При возрастании напряжений выше предела упругости деформация становится необратимой. При снятии нагрузки устраняется лишь упругая составляющая деформации, оставшаяся часть называется пластической деформацией.

Норм напряжение:

Составляющая напряжений, направленных по нормали к площадке ее действия.

Касат напряжение:

Составляющая напряжений, лежащих в плоскости сечения.

Правила знаков:

Нормальные напряжения σ принимаются положительными (т.е. σ>0), если они растягивают выделенный элемент бруса.

Касательные напряжения τ принимаются положительными (т.е. τ>0), если они стремятся повернуть рассматриваемый элемент бруса по ходу часовой стрелки.

При растяжении-сжатии

Внутренняя продольная сила N, которая стремится растянуть рассматриваемую частьбруса, считается положительной. Сжимающая продольная сила имеет отрицательный знак.

При кручении

Внутренний скручивающий момент T считается положительным, если он стремится повернуть рассматриваемую часть бруса против хода часовой стрелки, при взгляде на него со стороны внешней нормали.

При изгибе

Внутренняя поперечная сила Q считается положительной, в случае, когда она стремится повернуть рассматриваемую часть бруса по ходу часовой стрелки.

Внутренний изгибающий момент M положителен, когда он стремится сжать верхние волокна бруса.

Деформация при растяжении-сжатии Δl считается положительной, если длина стержняпри этом увеличивается.

При плоском поперечном изгибе

Вертикальное перемещение сечения бруса принимается положительным, если оно направлено вверх от начального положения.

Правило знаков при составлении уравнений статики

— для проекций сил на оси системы координат

Проекции внешних сил на оси системы координат принимаются положительными, если их направление совпадает с положительным направлением соответствующей оси.

— для моментов

Сосредоточенные моменты и моменты сил в уравнениях статики записываются с положительным знаком, если они стремятся повернуть рассматриваемую систему против хода часовой стрелки.

Правило знаков при составлении уравнений статики для неподвижных систем

При составлении уравнений равновесия статичных (неподвижных) систем (например, приопределении опорных реакций), последние два правила упрощаются до вида:

Проекции сил и моменты, имеющие одинаковое направление принимаются положительными, а соответственно проекции сил и моменты обратного направления – отрицательными.

ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ

Если все векторы напряжений параллельны одной и той же плоскости, напряженное состояние называется плоским (рис. 1). Иначе: напряженное состояние является плоским, если одно из трех главных напряжений равно нулю.

Рисунок 1.

Плоское напряженное состояние реализуется в пластине, нагруженной по ее контуру силами, равнодействующие которых расположены в ее срединной плоскости (срединная плоскость — плоскость, делящая пополам толщину пластины).

Направления напряжений на рис. 1 приняты за положительные. Угол α положителен, если он откладывается от оси х к оси у. На площадке с нормалью n:

(1)

при .

Нормальное напряжение σ_n положительно, если оно растягивающее. Положительное напряжение показано на рис. 1. Правило знаков дляпо формуле (1) то же самое, что для напряженийпо формуле (1).

Данное здесь правило знаков относится к наклонным площадкам. В статье «Объёмное напряженное состояние» сформулировано правило знаков для компонентов напряжений в точке, т. е. для напряжений на площадках, перпендикулярных осям координат. Это правило знаков принято в теории упругости.

Главные напряжения на площадках, перпендикулярных плоскости напряжений:

(2)

(Поскольку здесь рассматриваются только два главных напряжения, они обозначены через σ₁ и σ₂, хотя может оказаться, что σ₂<0, т. е. σ₂ не будет средним из трех главных напряжений). Угол α₁ составляемый нормалью к первой главной площадке с осью х, находится из равенства:

(3)

Наибольшее  и  наименьшее  касательные напряжения

(4)

Эти напряжения действуют на площадках, расположенных под углом 45° к первой и второй главным площадкам.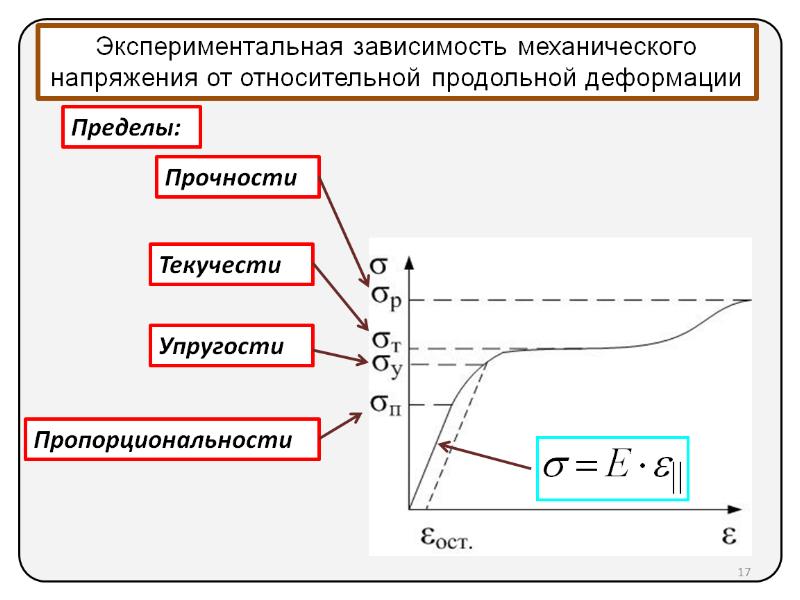

Если главные напряжения σ₁ и σ₂ имеют одинаковый знак, то наибольшее касательное напряжение действует на площадке, расположенной под углом 45° к плоскости напряжений (плоскости ху). В этом случае:

В стенке балки (здесь имеется в виду обычная балка, а не балка-стенка)  при ее изгибе силами реализуется частный случай плоского напряженного состояния. В стенках балки одно из нормальных напряжений σ_y равно нулю. В этом случае напряжения получатся по формулам (1), (2) и (4), если в этих формулах положить σ_y=0. Положение первой главной площадки определяется формулой (3).

РАСТЯЖЕНИЕ ПО ДВУМ НАПРАВЛЕНИЯМ (рис 2):

Рисунок 2.

При σ₁>0 и σ₂<0 

При σ₁>0 и σ₂>0 

При σ₁<0 и σ₂<0 

ЧИСТЫЙ СДВИГ (рис. 3)

Сопротивление материалов. Шпаргалка для студентовРоман Сиренко, 2009

3. Понятие о деформациях и напряжениях

Воздействие на тело внешних сил изменяет его внутренние силы. Деформация тела вызывает изменение расстояний между атомами, при этом возникающие дополнительные внутренние силы стремятся вернуть тело в первоначальное положение. Если неограниченно увеличивать действие внешних сил, то при определенном возрастании внутренних сил происходит разрушение тела. Чтобы произвести расчет на прочность, надо уметь определять внутренние силы, зная внешние. Для определения внутренних сил (или внутренних силовых факторов) используют метод сечения. Мысленно рассекаем твердое тело и отбрасываем одну из частей. Оставшаяся часть тела находится в положении равновесия под действием приложенных внешних сил и сил, приложенных к сечению (заменяющих воздействие отброшенной части тела). Теперь при помощи теоретической физики можно определить главный вектор действия внутренних сил по сечению (закон распределения этих сил установить сложно). Совмещая плоскость сечения с системой координат, имеем в сечении шесть силовых факторов: продольная сила N_z, пара поперечных сил Q_x,Q_y, изгибающие моменты M_x,M_y, крутящий момент M_z.

Соответственно видам внутренних силовых факторов различают четыре вида деформаций тела:

— если в сечении имеется только продольная сила — растяжение или сжатие;

— если в сечении возникают только поперечные силы — сдвиг;

— если в сечении возникают только изгибающие моменты — чистый изгиб, если кроме изгибающих моментов возникают поперечные силы — поперечный изгиб;

— если в сечении возникает крутящий момент — кручение.

Если в сечении действуют несколько силовых факторов, то возникает сложный вид деформации.

Как уже было сказано, при определении внутренних сил методом сечения считаем эти силы приложенными к центру тяжести сечения. На самом деле они распределены по всей поверхности сечения, и интенсивность внутренних силовых факторов может быть различной. Увеличение внешней нагрузки приводит к увеличению внутренней, заставляет возрастать интенсивность во всех точках сечения и может привести к разрушению элемента или возникновению остаточных деформаций. Таким образом, говоря о прочности тела, рассматривать надо не значение внутренних сил, а их интенсивность. Меру интенсивности внутренних сил характеризует напряжение. Для удобства математического и физического анализа напряжение рассматривают как совокупность двух компонент: вектора нормального напряжения и вектора касательно напряжения, являющихся соответственно его составляющими по нормали к сечению и касательно к его плоскости.

Напряжения и продольная деформация — Студопедия.Нет

При растяжении и сжатии

Растяжением или сжатием называется такой вид деформа­ции, при котором в любом поперечном сечении бруса возникает только продольная сила. Брусья с прямолинейной осью (прямые брусья), рабо­тающие на растяжение или сжатие, часто называют стержнями.

Рассмотрим невесомый, защемленный левым концом прямой брус, вдоль оси которого действуют активные силы F и 2F(рис. 19.1).

Части бруса постоянного сечения, заключенные между поперечными плоскостями, в которых приложены активные или реактивные силы, бу­дем называть участка-ми. Изображенный на рис. 19.1 брус состоит из двух участков.

Применив метод сече­ний, определим продоль­ные силы N₁и N₂на уча­стках. Рассечем брус на первом участке попереч­ным сечением 1—1.Во всех точках бруса будут

 

 

186

 

действовать внутренние распределенные силы, равнодействующая кото­рых определится из условия равновесия одной из частей бруса (например, правой от сечения):

откуда

Мы видим, что для равновесия оставленной части бруса в сечении

1—1необходимо приложить только силу N_1,направленную вдоль оси, т.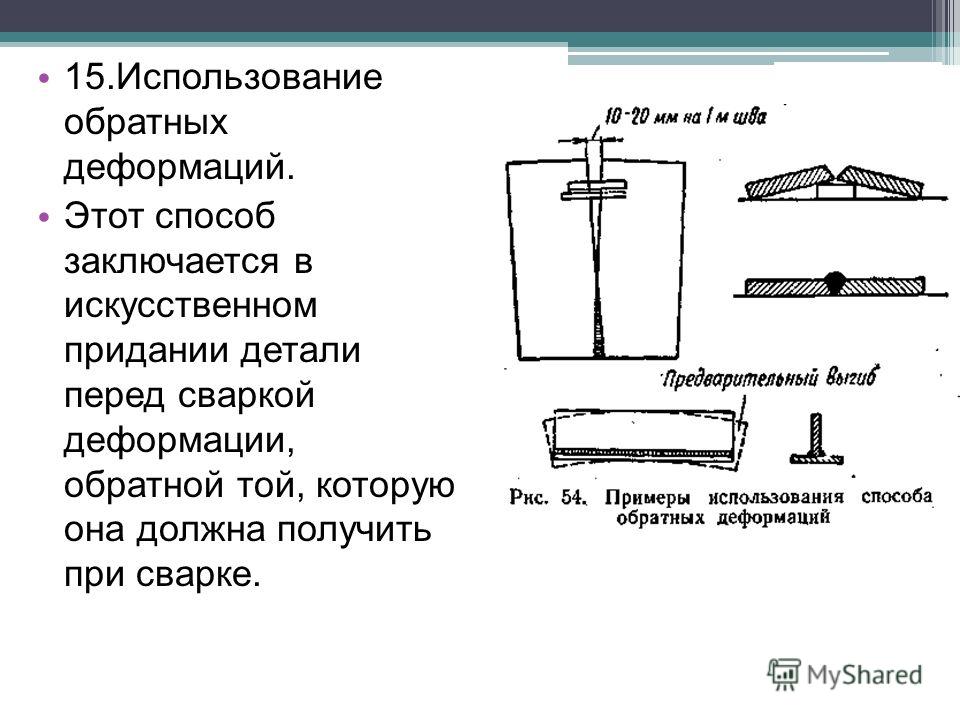 е. продольную силу.

Продольная сила есть равнодействующая внутренних нормальных сил, возникающих в поперечном сечении бруса. Нетрудно понять, что в сечении 2—2 на втором участке продольная сила будет иметь другое значение: N₂= 2F.Таким образом, продольная сила в поперечном сечении бруса чис­ленно равна алгебраической сумме внешних сил, расположенных по одну сторону сечения (имеется в виду, что все силы направлены вдоль оси бруса).

Очевидно, что в пределах одного участка продольная сила будет иметь постоянное значение. Следует помнить, что, рассматривая равно­весие части бруса, расположенной не справа, а слева от сечения, мы должны были ввести в уравнение равновесия реакцию защемленного конца, определенную путем рассмотрения равновесия всего бруса.

В дальнейшем растягивающие (направленные от сечения) продоль­ные силы мы будем считать положительными, а сжимающие (направ­ленные к сечению) — отрицательными.

Иначе говоря, если равнодействующая внешних сил, приложенных к левой части бруса, направлена налево, а приложенных к правой части — вправо, то продольная сила в данном сечении будет по­ложительной,и наоборот.

При изучении ряда деформаций мы будем мысленно представлять себе брусья состоящими из бесчисленного количества волокон, парал­лельных оси, и предполагать, что при деформации растяжения и сжатия волокна не надавливают друг на друга (это предположение называется гипотезой о ненадавливании волокон).

Если изготовить прямой брус из резины (для большей наглядности), нанести на его поверхности сетку продольных и поперечных линий и подвергнуть брус деформации растяжения, то можно отметить следую­щее: 1) поперечные линии останутся в плоскостях, перпендикулярных оси, а расстояния между ними увеличатся; 2) продольные линии останут­ся прямыми, а расстояния между ними уменьшатся.

Из этого опыта можно сделать вывод, что при растяжении справед­лива гипотеза плоских сечений и, следовательно, все волокна бруса удлиняются на одну и ту же величину.

187

 

 

Все сказанное выше позволяет сделать вывод, что при растяжении и сжатии в поперечных сечениях бруса возникают только нормальные на­пряжения, равномерно распределенные по сечению и вычисляемые по формуле

где N— продольная сила; А — площадь поперечного сечения. Очевидно, что при растяжении и сжатии форма сечения на напряжение не влияет.

В сечениях, близких к точкам приложения растягивающих или сжи­мающих сил, закон распределения напряжений по сечению будет более сложным, но пользуясь принципом смягченных граничных условий, мы будем этими отклонениями пренебрегать и считать, что во всех сечениях бруса напряжения распределены равномерно и что в сечении, где к брусу приложена вдоль оси сосредоточенная сила, значения продольной силы и напряжений меняются скачкообразно.

Для наглядного изображения распределения вдоль оси бруса про­дольных сил и нормальных напряжений строят графики, называемые эпюрами, причем для нормальных напряжений применяется то же пра­вило знаков, что и для продольных сил.

Пример 19.1.Построить эпюры продольных сил и нормальных напряжений для ступенчатого бруса, изображенного на рис. 19.2.

Решение. Разобьем брус на три участка. Границами участков являются сече­ния, в которых приложены внешние силы, и места изменения размеров попереч­ного сечения.

Для построения эпюры продольных сил N под рисунком бруса проводим ось эпюры, параллельную оси бруса. Величины продольных сил в произвольном масштабе откладываем перпендикулярно оси эпюры, причем положительные значения N (растяжение) откладываются вверх, а отрицательные (сжатие) — вниз от оси. Эпюру отштриховывают, как показано на рисунке. В точках прило­жения сил на эпюре N получаются скачкообразные изменения, причем величина «скачка» равна модулю приложенной в сечении бруса силы.

Применяя метод сечений, уста­навливаем, что во всех поперечных сечениях первого и второго участков действует продольная сила N₁ = —2F = N₂. Откладываем вниз от оси эпюры величину 2F в произвольном мас­штабе и проводим прямую, парал­лельную оси эпюры. В сечении С бруса приложена сила 3F.Применяя метод сечений, устанавливаем, что во всех поперечных сечениях третьего

участка действует продольная сила N₃ = F. Очевидно, что значение орди­наты эпюры продольных сил под заделкой равно реакции заделки. От­метим, что применяя метод сечений, выгоднее рассматривать равновесие части бруса, расположенной со сто­роны его свободного конца, в про­тивном случае необходимо заранее определять и вводить в уравнение равновесия реакцию заделки.

Для построения эпюры а определим нормальные напряжения на участках бруса. Тогда на первом участке нормальные напряжения будут ₁= -2F/2A = -F/A,на втором ₂ =-2F/A, на третьем ₃=F/A. Правила построения эпюры а те же, что и для эпюры N.

Для расчетов на прочность особый интерес представляют те сечения бруса, в которых напряжения являются по абсолютному значению максимальными. Эти сечения являются предположительно опасными. В нашем примере такими будут сечения бруса на втором участке.

Перейдем к рассмотрению деформаций. Представим себе прямой брус постоянного поперечного сечения А,длиной l, жестко защемленный одним концом и нагруженный на другом конце растягивающей силой F (рис. 19.3). Под действием этой силы брус удлинится на некоторую вели­чину l, которую назовем абсолютным удлинением. Отношение абсолютного удлинения l к первоначальной длине l назовем относи­тельным удлинением и обозначим :

 

Относительное удлинение  — число отвлеченное, иногда его выра­жают в процентах:

Вследствие деформации поперечные сечения бруса перемещаются в направлении оси. Взаимное перемещение двух сечений равно изменению длины части бруса, заключенной между этими сечениями.

Итак, деформация бруса при растяжении и сжатии характеризуется абсолютным и относительным удлинением или укорочением.

§19.2. Закон Гука при растяжении и сжатии

Напряжения и деформации при растяжении и сжатии связаны между собой зависимостью, которая называется законом Гука, по имени устано­вившего этот закон английского физика Роберта Гука (1635—1703).

189

Закон Гука при растяжении и сжатии справедлив лишь в определен­ных пределах нагружения и формулируется так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению.

Математически закон Гука можно записать в виде равенства:

 

Коэффициент пропорциональности Е характеризует жесткость мате­риала, т. е. его способность сопротивляться упругим деформациям растя­жения или сжатия, и называется модулем продольной упру­гости илимодулем упругости первого рода.

Модуль упругости и напряжение выражаются в одинаковых единицах:

Значения Е,МПа, для некоторых материалов:

Чугун……………………………………………….. (1,5…1,6) 10⁵

Сталь……………………………………………….. (1,96… 2,16) 10⁵

Медь…………………………………………………. (1,0…1,3) 10⁵

Сплавы алюминия…………………………….. (0,69…0,71) 10⁵

Дерево (вдоль волокон)………………………. (0,1…0,16) 10⁵

Текстолит…………………………………………. (0,06…0,1) 10⁵

Капрон ……………………………………………. (0,01…0,02) 10⁵

Если в формулу закона Гука подставим выражения

то получим

Произведение ЕА, стоящее в знаменателе, называется жестко­стью сечения при растяжении и сжатии; оно характеризует одно­временно физико-механические свойства материала и геометрические размеры поперечного сечения бруса.

Эта формула читается так: абсолютное удлинение или укорочение прямо пропорционально продольной силе, длине и обратно пропорцио­нально жесткости сечения бруса.

Отношение ЕА/l называется жесткостью бруса при растяже­нии или сжатии.

Приведенные выше формулы закона Гука применимы только для брусьев или их участков постоянного поперечного сечения, изготовлен­ных из одного материала и при постоянной продольной силе.

Для бруса, имеющего несколько участков, отличающихся материа­лом, размерами поперечного сечения, продольной силой, изменение дли­ны всего бруса равно алгебраической сумме удлинений и укорочений от­дельных участков:

Пример 19.2. На стальной ступен­чатый брус действуют силы F = 40 кН и R = 60 кН. Площади поперечных сече­ний равны А₁= 800 мм², А₂ = 1600 мм². Длины участков указаны на рис. 19.4; а = 0,2 м. Определить изменение дли­ны бруса двумя способами: 1) с помо­щью эпюры продольных сил; 2) с по­мощью принципа независимости дей­ствия сил. Принять Е = 2 10¹¹ Па.

Решение. 1-й способ. Разо­бьем брус на участки и, применяя ме­тод сечений, определим значения продольных сил на каждом из них:

N₁ = N₂= -40 кН (сжатие), N₃= 20 кН (растяжение). Строим эпюру продольных сил.

Для бруса, состоящего из нескольких участков, l= l ₁+ l ₂ + l ₃, где по закону Гука

— изменение длины первого участка; аналогич-

 

но,

 

Следовательно,

— изменение длин второго и третьего участков.

Подставив числовые значения с учетом знаков продольных сил, получим

 

откуда

 

Следовательно, брус укоротился на 0,15 мм.

2-й способ. Решим этот пример с помощью принципа независимости действия сил. Изменение длины бруса l будет складываться из укорочения l_F всего бруса под действием силы F и удлинения l_Rтретьего участка под действи­ем сипы R:

Вычислим каждое из этих слагаемых:

Подставляя числовые значения, получаем l_F= -0,225 мм.

Аналогично находим

Отсюда

Решая задачу двумя способами, мы получили один и тот же результат, что свидетельствует о правильности решения.

191

Поперечная деформация

При растяжении и сжатии

Описанный в § 19.1 опыт с резиновым брусом показывает, что попе­речные размеры сечения при растяжении уменьшаются, а при сжатии увеличиваются. Это характерно для растяжения и сжатия всех материа­лов. Опытным путем установлено, что при одноосном растяжении или сжатии отношение относительных поперечной и продольной деформаций есть для данного материала величина постоянная. Впервые зависимость между относительной поперечной ‘ и относительной продольной е деформа­циями была установлена французским ученым Пуассоном (1781—1840). Эта зависимость имеет следующий вид:

 

где v — коэффициент поперечной деформации, называемый к о э ф ф и -циентом Пуассона.

Нетрудно понять, что v — величина безразмерная.

Коэффициент Пуассона, как и модуль упругости первого рода, зави­сит только от материала и характеризует его упругие свойства. При рас­тяжении и сжатии коэффициент Пуассона полагают одинаковым.

Значения v для некоторых материалов:

Пробка……………. 0,00        Латунь……………….. 0,32…0,42

Чугун……………… 0,23…0,27  Свинец……………….. 0,42

Сталь …………….. 0,24…0,30  Каучук ………………. 0,47

Медь………………. 0,31-0,34 Парафин ……………. 0,5

Пример 19.3. Стальной цилиндр (рис. 19.5) длиной l = 100 мм и диаметром d = 40 мм при сжатии укорачивается до размера l₁= 99,9 мм, а диаметр его увели­чивается до размера d₁ = 40,01 мм. Найти коэффициент Пуассона v.

Решение. Определим относительную продоль­ную и поперечную деформацию | | и | ‘|, если l= l –

 – l₁= 0,1 мм , a d= d₁ — d = 0,01 мм, тогда

l/l=| |, d/d=| ‘|.

 Отсюда коэффициент Пуассона

v = | ‘/ |= l d/(d l).

 Подставляя числовые значения, получим

v = 100 0,01/(40 0,1) = 0.25.

Диаграмма растяжения

Низкоуглеродистой стали

Механические характеристики материалов, т. е. величины, характе­ризующие их прочность, пластичность, упругость, твердость, а также уп­ругие постоянные Е и v, необходимые конструктору для выбора материа­лов и расчетов проектируемых деталей, определяют путем механических испытаний стандартных образцов, изготовленных из исследуемого мате­риала.

Большая заслуга в установлении единообразных во всем мире мето­дов испытания материалов принадлежит русскому профессору Н. А. Беле-любскому (1845—1922) — президенту Международного общества испы­тания материалов.

Вопросы проведения лабораторных испытаний материалов в настоя­щей книге не излагаются, с ними читатель может ознакомиться в специ­альных учебных пособиях.

В данном параграфе мы подробно рассмотрим диаграмму, получен­ную в процессе наиболее распространенного и важного механического испытания, а именно испытания на растяжение низкоуглеродистой стали (например, стали СтЗ) при статическом нагружении.

В процессе этого испытания специальное устройство испытательной машины автоматически вычерчивает диаграмму, выражающую зависи­мость между растягивающей силой и абсолютным удлинением, т. е. в координатах (F, l).Для изучения механических свойств материала неза­висимо от размеров образца применяется диаграмма в координатах «на­пряжение—относительное удлинение» ( , ). Эти диаграммы отличаются друг от друга лишь масштабами.

Диаграмма растяже­ния низкоуглеродистой стали представлена на рис. 19.6. Эта диаграмма име­ет следующие характер­ные точки.

Точка А соответствует пределу пропорциональ­ности.

Пределом про-порциональности _пц называется то наибольшее напряжение, до которого деформации растут про­порционально нагрузке,

 

т. е. справедлив закон Гука (для стали СтЗ _пц 200 МПа).

Точка А практически соответствует и другому пределу, который на­зывается пределом упругости.

Пределом упругости уп называется то наибольшее напря­жение, до которого деформации практически остаются упругими.

Точка С соответствует пределу текучести.

Пределом текучести _т называется такое напряжение, при котором в образце появляется заметное удлинение без увеличения на­грузки (для стали СтЗ _т 240 МПа).

При достижении предела текучести поверхность образца становится матовой, так как на ней появляется сетка линий Людерса—Чернова, на­клоненных к оси под углом 45°. Эти линии впервые были описаны в 1859 г. немецким металлургом Людерсом и независимо от него в 1884 г. русским металлургом Д. К. Черновым (1839—1921), предложившим использовать их при экспериментальном изучении напряжений в сложных деталях.

Предел текучести является основной механической характеристикой при оценке прочности пластичных материалов.

Точка В соответствует временному сопротивлению или пределу прочности.

Временным сопротивлением а„ называется условное на­пряжение, равное отношению максимальной силы, которую выдерживает образец, к первоначальной площади его поперечного сечения (для стали СтЗ _В 400 МПа).

При достижении временного сопротивления на растягиваемом об­разце образуется местное сужение — шейка, т. е. начинается разрушение образца.

В определении временного сопротивления говорится об условном напряжении, так как в сечениях шейки напряжения будут больше.

Пределом прочности _пчназывается временное со­противление образца, разрушающегося без образования шейки. Предел прочности является основной механической характеристикой при оценке прочности хрупких материалов.

Точка D соответствует напряжению, возникающему в образце в мо­мент разрыва во всех поперечных сечениях, кроме сечений шейки.

Точка М соответствует напряжению, возникающему в наименьшем поперечном сечении шейки в момент разрыва. Это напряжение можно назвать напряжением разрыва.

С помощью диаграммы растяжения в координатах ( , ) определяем модуль упругости первого рода:

где — масштаб напряжении; — масштаб относительных удлинении;

194

— угол, который составляет с осью абсцисс прямая линия диаграммы до предела пропорциональности.

Для большинства углеродистых сталей предел пропорциональности можно приблизительно считать равным половине временного сопротив­ления.

Деформация образца за пределом упругости состоит из упругой и остаточной, причем упругая часть деформации подчиняется закону Гука и за пределом пропорциональности (см. рис. 19.6). Если нагрузку снять, то образец укоротится в соответствии с прямой TF диаграммы. При повторном нагружении того же образца его деформация будет соответст­вовать диаграмме FTBD.Таким образом, при повторном растяжении образца, ранее нагруженного выше предела упругости, механические свойства материала меняются, а именно: повышается прочность (предел упругости и пропорциональности) и уменьшается пластичность. Это явление называется наклёпом.

В некоторых случаях наклеп нежелателен (например, при пробивке отверстий под заклепки увеличивается возможность появления трещин возле отверстий), в других случаях наклеп создается специально (напри­мер, цепи подъемных машин, арматура железобетонных конструкций, провода, тросы подвергаются предварительной вытяжке за предел теку­чести). Проволока, полученная волочением, в результате наклепа имеет значительно большую прочность, чем точеный образец из того же мате­риала.

Степень пластичности материала может быть охарактеризована (в процентах) остаточным относительным удлинением  и остаточным относительным сужением шейки образца после разрыва:

где l_o — первоначальная длина образца; l_р — длина образца после разры­ва; А_o— первоначальная площадь поперечного сечения образца; А_ш—площадь наименьшего поперечного сечения шейки образца после разрыва.

Чем больше  и , тем пластичнее материал. Материалы, обладаю­щие очень малой пластичностью, называют хрупкими. Диаграмма растяжения хрупких материалов не имеет площадки текучести, у них при разрушении не образуется шейка.

Диаграмма сжатия стали до предела текучести совпадает с диаграм­мой растяжения, причем результаты испытаний сталей на растяжение и сжатие равноценны.

Результаты испытаний на растяжение и сжатие чугуна значитель­но отличаются друг от друга; предел прочности при растяжении в

195

3…5 раз ниже, чем при сжа­тии. Иными словами, чугун значительно хуже работает на растяжение, чем на сжа­тие.

Отметим, что ярко выра­женную площадку текучести имеют только диаграммы растя­жения низкоуглеродистой стали и некоторых сплавов цветных металлов. На рис. 19.7 показан для сравнения вид диаграмм растяжения сталей с различным содержанием углерода; из рисунка видно, что с повышением процента содержания углерода увеличивается проч­ность стали и уменьшается ее пластичность.

Для пластичных материалов, диаграммы растяжения которых не имеют ярко выраженной площадки текучести (средне и высокоугле­родистые, легированные стали) или совсем ее не имеют (медь, дюралю­миний), вводится понятие условного предела текучести — напряжения, при котором относительное остаточное удлинение об­разца равно 0,2%. Условный предел текучести также обозначим _т (иногда его обозначают _0,2).

Следует отметить, что деление материалов на пластичные и хрупкие условно, так как в зависимости от характера действующей нагрузки хруп­кий материал может получить пластические свойства и, наоборот, пла­стичный материал приобретает свойства хрупкого. Так, например, деталь из пластичного материала при низкой температуре или при ударной на­грузке разрушается без образования шейки, как хрупкая.

Напряжение и деформация: механические свойства материалов

Каждый компонент в системе линейного перемещения испытывает ту или иную форму нагрузки из-за приложенных сил или движения. Реакция компонента на эти нагрузки описывается его механическими свойствами.

Для компонентов, подверженных растяжению или сжатию, таких как несущие шарики и ролики, валы, установленные вертикально, или крепежные и соединительные детали, механические свойства напряжения и деформации играют важную роль в определении того, может ли компонент выдерживать условия нагрузки приложения .

Существует пять основных типов нагружения: сжатие, растяжение, сдвиг, кручение и изгиб.

---

Напряжение — это сила, приложенная к материалу, деленная на площадь поперечного сечения материала.

σ = напряжение (Н / м ² , Па)

F = сила (Н)

A ₀ = исходная площадь поперечного сечения (м ² )

Деформация — это деформация или смещение материала в результате приложенного напряжения.

ε = деформация

L = длина после приложения нагрузки (мм)

L ₀ = исходная длина (мм)

Примечание. Изменение длины материала (L — L ₀ ) иногда обозначается как δ.

---

Наиболее распространенный способ анализа взаимосвязи между напряжением и деформацией для конкретного материала — это диаграмма «напряжение-деформация».

Диаграмма «напряжение-деформация» дает ценную информацию о том, какое усилие может выдержать материал, прежде чем произойдет остаточная деформация или разрушение.

Многие материалы демонстрируют пропорциональную зависимость между напряжением и деформацией до определенной точки, называемую пределом пропорциональности, обозначенную здесь точкой «А». Эта зависимость между напряжением и деформацией известна как закон Гука, и в этой области наклон кривой зависимости напряжения от деформации называется модулем упругости (он же модуль Юнга), обозначаемым E.

Модуль упругости — это, по сути, мера жесткости и один из факторов, используемых для расчета прогиба материала под нагрузкой.

Сразу за пределом пропорциональности находится предел упругости, при котором материал переходит от упругого поведения, при котором любая деформация, вызванная приложенным напряжением, меняется на противоположную при снятии силы, к пластическому поведению, при котором деформации, вызванные напряжением, сохраняются даже после воздействия напряжения. удален. Для многих материалов предел пропорциональности и предел упругости одинаковы или почти равны. (На представленной здесь кривой напряжения-деформации предполагается, что предел пропорциональности и предел упругости одинаковы.)

---

До тех пор, пока приложенные напряжения ниже пропорционального предела, отношения напряжение-деформация одинаковы, независимо от того, находится ли материал при растяжении или сжатии.

---

Предел текучести, обозначенный здесь как точка «С», — это точка, в которой деформация увеличивается быстрее, чем напряжение (называемое «деформационным упрочнением»), и материал испытывает некоторую остаточную деформацию.

Для материалов, которые не имеют четко определенного предела текучести или предел текучести которых трудно определить, используется предел текучести со смещением, обозначенный здесь точкой «B».Предел текучести со смещением — это напряжение, которое вызовет определенную остаточную деформацию (обычно 0,2 процента). Его можно найти, проведя линию, которая пересекает ось X (деформация) в 0,002 и проходит параллельно линии напряжения-деформации (наклон = E). Точка, в которой эта линия пересекает кривую напряжения-деформации, является пределом текучести смещения.

Наконец, в точке «D», где кривая начинает падать, достигается предел прочности материала на разрыв. Эта точка обозначает максимальное напряжение, которое может быть приложено к растянутому материалу до того, как произойдет разрушение.

---

Термин «прочность» может использоваться с различными свойствами материала (предел прочности на разрыв, предел текучести, предел прочности на сдвиг и т. Д.). Но независимо от описываемого свойства, «прочность» обычно относится к сопротивлению материала разрушению, будь то из-за разрушения или чрезмерной деформации.

---

Обратите внимание, что в приведенном выше обсуждении исходная площадь поперечного сечения и длина (до того, как произошла деформация) использовались для расчета напряжения и деформации соответственно.Таким образом, диаграмма упоминается как «диаграмма напряжения-деформации Engineering ». Но по мере деформации материала изменяется его площадь поперечного сечения и длина. Диаграмма напряжение-деформация, которая использует мгновенные значения площади поперечного сечения и длины для определения напряжения и деформации, называется «диаграммой деформации-деформации истинной ».

Для большинства применений достаточно инженерной диаграммы «напряжение-деформация», поскольку разница между техническими и истинными версиями очень мала ниже предела текучести материала.

Напряжение и деформация

Количественные понятия: тригонометрия, построение графиков

---

^{доктором Кэрол Орманд (Университет Висконсина — Мэдисон) и доктором Эриком Баером (Общественный колледж Хайлайн)}
Перейти к: Стресс, напряжение и т. Д. конструкции | Условия деформации | Неисправности | Аналоги | Примеры обучения | Ресурсы

Основные понятия

Есть 5 основных концепций, с которыми учащиеся борются, думая о стрессе и деформации:

1. скалы деформируются,
2. напряжение вызывает деформацию и деформацию приводит к конструкциям,
3. различных физических условий создают разные конструкции,
4. , предполагающий напряжение от неисправностей, и
5. взаимосвязь аналогов и реальности.

Скалы деформируются

Многим ученикам трудно понять, что камни могут гнуться или ломаться. У них также могут быть трудности с представлением сил, необходимых для складывания или разлома горных пород, или с пониманием того, что кажущаяся постоянной Земля может резко измениться со временем. Особенно это касается студентов, проживающих в тектонически стабильных районах. Если учащиеся должны понимать основы напряжения и деформации, они должны преодолеть этот барьер, поскольку будет трудно изучить причины и условия деформации, если учащиеся не могут понять деформацию.Часто бывает полезно попросить студентов создать аналоговые модели структур, представленных на фотографиях горных пород или ручных образцах.

Вот изображение структуры, известной как будинаж (названный в честь французского слова кровяная колбаса — обратите внимание на структуру, похожую на колбасу). Можете ли вы сделать аналогичную структуру, используя Silly Putty®? Какая скорость деформации необходима для получения чего-то подобного (получите ли вы тот же результат, если будете разбирать это быстро или медленнее)? Будет ли лучше работать, если ваша Silly Putty® теплая или холодная? Как вы думаете, такой же результат будет с PlayDoh® или тестом для печенья? Влияет ли количество Silly Putty® на то, насколько легко вы можете воспроизвести структуру? Все эти условия могут быть преобразованы в горные породы — скорость, с которой они деформируются, температура, тип материала, масштаб — и влияют на типы структур, которые обнаруживаются в летописи горных пород.

Чтобы показать учащимся, что горные породы деформируются, можно использовать фотографии и образцы реальных скал с разломами и складками в различных масштабах. Есть несколько хороших коллекций этих типов изображений, таких как Всемирный банк изображений AGI Earthscience, коллекция Мартина Миллера или набор слайдов National Geophysical Data Center Faults.

Напряжение вызывает деформацию, деформация вызывает конструкции

Многие геологи считают важным для начинающих студентов понять, что видимые структуры отражают напряжение и физические условия на Земле.В результате ключевыми понятиями становятся различия между напряжением, деформацией и структурами, образованными во время деформации.

• Напряжение — это сила, действующая на скалу на единицу площади. Он имеет те же единицы измерения, что и давление, но также имеет направление (т. Е. Вектор, как и сила). Существует три типа напряжения: сжатие, растяжение и сдвиг. Напряжение может вызвать деформацию, если ее достаточно, чтобы преодолеть силу объекта, находящегося под нагрузкой.
• Деформация — это изменение формы или размера в результате приложенных сил (деформации).Скалы деформируются только тогда, когда подвергаются нагрузке. Любой камень можно напрячь. Деформация может быть упругой, хрупкой или пластичной. Пластическая деформация также называется пластической деформацией.
• Структуры в геологии — это деформационные особенности, возникающие в результате постоянной (хрупкой или вязкой) деформации. Примеры включают складки и разломы. Геологи используют эти особенности, чтобы определить тип напряжения, которое испытывала горная порода, а также условия нагрузки, которой она подверглась (или которой она подвергалась, в зависимости от вашей точки зрения).

После демонстрации изображений деформированных горных пород, предоставление студентам возможности создавать свои собственные «структуры» из пластилина Play-Doh®, Silly Putty® или другого геологического аналога, помогает им понять концепции, лежащие в основе напряжений и напряжений, и позволяет им исследовать взаимосвязи между напряженные, деформированные и деформационные конструкции. Студенты могут поэкспериментировать с типами напряжения и скоростью деформации, необходимыми для того, чтобы аналоги сломались или согнулись. В качестве альтернативы они могут использовать аналогичные конструкции для определения напряжений и скоростей деформации после создания «конструкции».См. Rocks deform выше, где учащиеся создают будины.

Напряжение, напряжение и структура начинаются с одних и тех же трех букв, но означают совершенно разные вещи. Эти слова также используются в геологии иначе, чем в английском языке, что может вызвать путаницу. Однако вот некоторые приемы, которые я использую, чтобы запомнить:

• Напряжение равно давлению. Когда вы находитесь под давлением, вы испытываете стресс!
• Стресс может происходить без напряжения, но напряжение не может происходить без напряжения.

Посмотрите на этот камень, который я сжимаю в руке.

• Это подчеркнуто? (Да, находится под давлением.)
• Напряжено? (Нет, форма не изменилась.)

А теперь посмотрите на этот камень со складкой внутри.

• Под напряжением? (Нет, не под давлением).
• Напрягает? (Нет, в настоящее время он не меняет форму.)
• Есть ли структура? (Да, складка есть.)

В дополнение к Silly Putty® и Play-Doh®, деревянные блоки с втянутыми слоями или резервуар для сжатия / сжатия, наполненный слоистым песком или хлопьями для завтрака, также хорошо моделируют структурные особенности.Однако аналоги трудно масштабировать соответствующим образом (как во времени, так и в пространстве) до гигантских масштабов, в которых формируются геологические структуры. Студенты могут по-прежнему испытывать трудности с пониманием огромного масштаба сил, необходимых для сгибания или разрушения породы, и длительных временных масштабов, необходимых для создания структур. Убедитесь, что вы объяснили своим ученикам, что эти подводные камни существуют. Более подробные идеи для аналогов доступны на веб-странице аналоговых материалов для преподавания структурной геологии.

После того, как учащиеся усвоили взаимосвязь между напряжением, деформацией и структурой, я составляю таблицу 3 x 2 с различными структурами, которые формируются в различных условиях напряжения и деформации.Затем я приступаю к заполнению таблицы с помощью студентов.

Давайте посмотрим, какие особенности проявляются в различных стрессовых условиях и при разных стилях деформации. Сделаем это, сделав стол. Какие три типа стресса? Сжатие, растяжение и сдвиг. Итак, каковы 2 типа постоянной деформации? Пластичный и хрупкий. Давайте составим таблицу из трех столбцов на две строки и заполним ее соответствующими структурами! Когда мы закончим, у нас должно быть 6 видов деформаций.

Теперь посмотрим, сможете ли вы сделать каждый из них с помощью Play-Doh® или блоков.

Различные условия приводят к разным стилям деформации

Есть много факторов, которые влияют на стиль деформации в горной породе, включая давление, температуру, состав породы, наличие или отсутствие флюидов, тип напряжения, скорость напряжения и другие. Однако тип стресса, уровень стресса и температура могут быть наиболее важными факторами для большинства студентов начального уровня.

Silly Putty® — это материал, который, как и камни, может деформироваться пластически или хрупко. Что контролирует его деформацию?

• Температура: холодная Silly Putty легко сломается, а теплая Silly Putty очень пластична.
• Скорость деформации: Если я быстро разорву его, он сломается, но если я потяну медленно, он растянется (деформируется пластически).
• Тип стресса: наконец, выберите сильного ученика и попросите его или ее попытаться сломать глупую замазку с помощью сжимающего напряжения.Как видите, это практически невозможно. Теперь попросите ученика попытаться сломать его с помощью напряжения. Это намного проще. Большинство материалов легче разрушается (или иначе деформируется) при растяжении, чем при сжатии; мы говорим, что они слабее при растяжении или сильнее при сжатии.

Температура, скорость деформации и тип напряжения также являются ключевыми факторами деформации в ледниках. Это дает возможность вернуться к этим концепциям позже в семестре.

Связь разломов с напряжением — висячие стены, опорные стены и различные типы разломов

Одна из целей структурной геологии — связать природу деформации с вызвавшим ее напряжением.Следовательно, важно, чтобы учащиеся могли различать нормальные разломы (вызванные растяжением) и обратные разломы (генерируемые сжатием).

Деревянные блоки — ценный инструмент для обучения нормальным и обратным неисправностям. Используя три блока, вырезанных под углом, можно создавать горсты и грабены. Раздвиньте блоки, чтобы создать грабен; столкните их вместе, чтобы получился горст. Преимущество использования 3 блоков состоит в том, что студенты могут видеть, что важна не ориентация разлома, а движение по разлому.Поскольку они могут видеть, расширяю ли я блоки или сжимаю их, они развивают интуитивное чувство разницы между нормальными и обратными разломами. Тем не менее, студентам, как правило, все же необходимо изучить разницу между нависающей стеной и подошвой разлома, чтобы иметь возможность точно определить, является ли разлом нормальным или обратным, и какое напряжение вызвало его.

Разломы — это места, где скалы были разрушены и смещены. Нередко флюиды протекают вдоль разлома во время деформации, оставляя ценные минералы вдоль разлома.В результате многие шахты строятся вдоль поверхностей разломов. Из-за этого одна сторона разлома называется висячей стеной (поверхность, на которой будет висеть фонарь шахтера), а одна сторона называется подошвой (поверхность, по которой будет ходить шахтер).

Вот другой способ подумать об этом: висячий стеновой блок всегда находится выше плоскости разлома, а нижний стеновой блок всегда ниже плоскости разлома. Чтобы в этом убедиться, поставьте точку на разломе и нарисуйте вертикальную стрелку, указывающую вверх.Эта стрелка указывает на висящую стену. Стрелка, указывающая прямо вниз, указывает на подножку. Взгляните на слайд, на котором показаны неисправность и стрелки, указывающие движение. Некоторые студенты думают, что ступня похожа на ступню. Видите, как подвесная стена опирается или висит на стене для ног?

Как только учащиеся поймут разницу между висячей стеной и стенкой для ног, большинству из них не составит труда вспомнить, что при обратном разломе висячая стена движется вверх, указывая на сжатие, а в нормальном разломе висящая стена движется вниз, указывая на расширение.

Как ваши ученики могут видеть из этих блочных моделей, горизонтальные силы могут заставлять горные породы перемещаться по разломам, расположенным под углом к ​​слоистым породам. Исходя из этой идеи, ваши ученики могут использовать некоторые базовые тригонометрические функции для изучения взаимосвязи между горизонтальной деформацией (степенью растяжения или сокращения в горизонтальном направлении) и смещением на поверхности разлома (величиной движения самого разлома). Поскольку это соотношение зависит от угла разлома по отношению к горизонтали, угол разлома является критическим компонентом того, как разломы компенсируют сокращение или расширение.

Разлом Сиэтла — это большой обратный разлом, который проходит через и под Сиэтлом, штат Вашингтон, столичной зоной и ее почти 2 миллионами жителей. Разлом Сиэтла вмещает около 1 миллиметра сокращения в год. Однако, поскольку сама плоскость разлома плохо обнажена и / или не различима на сейсмических профилях, мы не знаем, какой угол этот разлом образует к горизонтали. Если повреждение малоугловое, примерно под 25 градусами от горизонтали, то для компенсации укорочения 1 мм он должен сместиться на 1.В среднем 1 мм / год. Однако, если он находится под более крутым углом в 60 градусов, ему потребуется сдвинуть в среднем 2 мм в год. Поскольку смещение разлома является основным фактором при определении силы землетрясения (см. Страницу о землетрясениях), разлом Сиэтла должен перемещаться либо вдвое чаще, либо иметь гораздо более сильные землетрясения, если он находится под крутым углом. Косинус (A) = скорость укорочения по горизонтали / скорость смещения разлома, где A — угол разлома к горизонтали. Решая для скорости смещения разлома, мы получаем скорость смещения = скорость укорочения / Cos (A).Таким образом, для разлома под углом 25 градусов, который соответствует сокращению на 1 мм / год, скорость смещения будет 1 / cos (25) мм / год, или 1,1 мм / год. Для разлома под углом 60 градусов скорость смещения будет 1 / cos (60) мм / год или 2 мм / год.

Отношение аналогов к реальной Земле

Мы часто используем аналогии и аналогичные материалы (Silly Putty, песок, деревянные блоки и т. Д.), Чтобы проиллюстрировать концепции напряжения, деформации и деформации горных пород. Однако студентам иногда сложно соотнести эти материалы и их поведение с Землей и реальными камнями.Для этих студентов может быть полезно обсудить скорость и величину деформации Земли и различия между горными породами и аналогичными материалами. Например, породы на границах плит часто испытывают деформацию на несколько сантиметров в год, но сил, действующих на них, достаточно, чтобы сдвинуть континенты. Размер и медленность этих процессов являются важным понятием для коммуникации, даже если они имеют масштаб, который практически невозможно понять. Я иногда говорю студентам, что их ногти растут примерно с той же скоростью, с которой движутся пластины, чтобы помочь им преодолеть эту трудность.

Пластины двигаются примерно с той же скоростью, что и ногти, на несколько сантиметров в год. Хотя это кажется медленным, через длительные периоды времени это действительно складывается. Например, если вы позволите ногтям расти в течение 100 миллионов лет, их длина составит около 4000 километров!

Обучающие примеры

• Соединения в аналоге кукурузного крахмала
Осушенная смесь кукурузного крахмала и воды обеспечивает интерактивное знакомство с суставами и наборами суставов. Студенты интерпретируют относительный возраст, исследуют углы пересечения, используют текстуры поверхности для определения направления распространения и оценивают роль дефектов в зарождении суставов.
• Основы перелома: простой аналог
В этом упражнении учащиеся делают небольшие надрезы (ядра трещин) в продуктах из плавленого сыра, а затем прикладывают усилия, перпендикулярные или параллельные надрезам, чтобы увидеть, как растут трещины. Как ни странно (или нет, в зависимости от предыдущих мыслей о сыре), плавленый сыр ломается почти так же, как однородные породы.
• Развитие систем нормальных разломов при прогрессирующей деформации
Это упражнение основано на фильмах QuickTime и цветных цифровых фотографиях, полученных в результате экспериментов в песочнице, которые производят нормальные разломы в различных граничных условиях после экспериментов, разработанных Кеном МакКлеем.Студенты просматривают специально отредактированные фильмы, чтобы получить представление об эволюции нормальных систем неисправностей. Затем они исследуют формирование и эволюцию системы разломов для конкретных структурных условий, отслеживая и маркируя отдельные разломы на серии фотографий, сделанных через регулярные промежутки времени во время эксперимента. Это упражнение помогает учащимся развить понимание возникновения, распространения, вращения и деактивации разломов во время прогрессирующей деформации.
• Анализ трещин тротуаров
Используя трещины на тротуарах в качестве аналога естественных обнажений, студенты учатся проводить систематические наблюдения, измерять ориентацию и расположение трещин, обрабатывать и анализировать данные, а также рассматривать некоторые кинематические и динамические вопросы, касающиеся происхождения и значимости трещин.

ресурсов

• Преподавание структурной геологии в 21 веке
Этот сайт содержит множество ресурсов для преподавателей, преподающих структурную геологию на бакалавриате. Вы найдете ссылки на мероприятия и задания, Интернет и компьютерные ресурсы, полезные статьи и карты, презентации с семинара лета 2004 г. по преподаванию структурной геологии, рабочие группы и дискуссионный форум, а также множество творческих идей для преподавания структурной геологии.
• 3D визуализации деформации конструкций
GeoBlocks 3D, созданный Стивом Рейнольдсом, содержит интерактивные фильмы QuickTime Virtual Reality (QTVR), исследующие трехмерную природу геологии, в частности геологические структуры внутри блоков. Вы можете вращать блоки, делать их частично прозрачными, чтобы увидеть их внутреннюю структуру, прорезать или разрушать их, смещать разломы и многое другое.
• Структурная геология горных пород и областей (вводная глава)
Этот учебник Дэвиса и Рейнольдса является наиболее широко используемым учебником по структурной геологии согласно недавнему исследованию.Вводная глава может быть полезна преподавателям в размышлениях о том, как преподавать этот раздел вводного класса, поскольку в ней рассматриваются три основных способа изучения деформаций геологами-строителями: геометрический анализ, кинематический анализ и динамический анализ.
• Интернет-страница Стива Рейнольдса
Эта страница содержит множество инструментов визуализации и другие ресурсы, разработанные и собранные Стивом Рейнольдсом, профессором геологии в Университете штата Аризона.
• Ресурсы курса структурной геологии в Интернете
Каталог курсов с онлайн-ресурсами или веб-страницами

Напряжение и деформация — растягивающее напряжение, растягивающая деформация, энергия упругой деформации, разрушающее напряжение, пластичность, хрупкость

Напряжение

Напряжение, приложенное к материалу, — это сила, приложенная к материалу на единицу площади.Максимальное напряжение, которое может выдержать материал до разрушения, называется разрывным напряжением или пределом прочности при растяжении.

Растяжение означает, что материал находится под напряжением. Действующие на него силы пытаются растянуть материал. Сжатие — это когда силы, действующие на объект, пытаются его раздавить.

Приведенное ниже уравнение используется для расчета напряжения.

напряжение = напряжение, измеренное в Нм ^-2 или паскалях (Па)
F = сила в ньютонах (Н)
A = площадь поперечного сечения в м ²

Штамм

Отношение удлинения к исходной длине называется деформацией. Он не имеет единиц измерения, поскольку представляет собой отношение двух длин, измеренных в метрах.

деформация = деформация не имеет единиц
DL = удлинение, измеренное в метрах
L = исходная длина, измеренная в метрах

График напряжение-деформация для пластичного материала (например, меди)

• L = предел пропорциональности, до этого момента действует закон Гука.
• E = предел упругости, за пределами этой точки материал постоянно растягивается и не возвращается к своей исходной длине. Упругое поведение — это когда материал возвращается к своей исходной длине, пластическое поведение — это когда растянутый материал не возвращается к своей исходной длине.
• Y = предел текучести, за пределами этой точки небольшое увеличение силы приводит к значительному увеличению длины.
• B = предел прочности / разрывное напряжение, в этой точке материал разрушается.

График напряжение-деформация для хрупкого материала (например, стекла)

Энергия упругой деформации (энергия, запасенная в растянутой проволоке или пружине)

Энергия, запасенная в растягивающейся проволоке или пружине, — это площадь под графиком «сила-растяжение», как мы можем видеть в уравнении ниже.

• E = энергия упругой деформации в джоулях (Дж)
• F = сила в ньютонах (Н)
• DL = изменение длины в метрах (м)

Резина растяжка

Когда резина растягивается и выделяется энергия, теряется в виде тепла, и это называется гистерезисом. Площадь между двумя линиями — это потеря энергии на единицу объема.

3.3 Материальное уравнение: отношения напряжения и деформации

3.3 Материальное уравнение: отношения напряжения и деформации Подразделы

---

Материальные уравнения говорят нам, как твердое тело деформируется (во времени) в ответ на напряжения, изменения температуры и, в частности, изменения порового давления.Выбор определяющего уравнения зависит от свойств материала, величины изменения деформации, величины напряжений и скорости нагружения среди других факторов.

Рисунок 3.9: Пример деформаций, вызванных приложенным напряжением.

Простейшим определяющим соотношением для твердых тел является линейная упругость, в которой напряжения и деформации линейно связаны постоянными коэффициентами. Примеры на рисунке 3.10 соответствуют приложениям линейной упругости в различных измерениях:

Рисунок 3.10: От закона Гука к обобщенной трехмерной линейной упругости.

Рассмотрим призматическое твердое тело длиной, к которому приложено напряжение на верхней грани 3 (рисунок 3.11). Нижняя грань не может двигаться в направлении 3, но может скользить вбок. Четыре других грани могут двигаться во всех направлениях. Обратите внимание, что верхняя грань также может деформироваться в направлениях 1 и 2.Модуль Юнга определяется как отношение приложенного напряжения и результирующая деформация (в направлении приложенного напряжения)

(3.13)

Твердое тело, скорее всего, будет увеличиваться в направлении, перпендикулярном приложенному напряжению. Коэффициент Пуассона (греческая буква ню) определяется как (-1), умноженное на отношение деформации, перпендикулярной приложенному напряжению. (или ) и деформации в направлении приложенного напряжения

(3.14)

Эти два коэффициента являются двумя коэффициентами, обычно используемыми в качестве констант упругости в механике сплошных сред. Позже мы увидим, что в геологической среде мы почти никогда не находим условий бокового «неограниченного» нагружения напряжением, подобных показанному на Рисунке 3.11.

Рисунок 3.11: Безграничное напряженное нагружение (сжатие) линейно-упругого изотропного твердого тела. Поскольку твердое тело изотропно, те же уравнения справедливы для сжатия в любом другом направлении, а также для растяжения.

Реальное поведение горных пород отличается от предположения о линейной упругости. На рис. 3.12 показано схематическое изображение типичного испытания на неограниченную нагрузку. На рисунке показано осевое напряжение по вертикальной оси и осевая деформация. по горизонтальной оси. Часто каменные пробки не идеально параллельны или могут иметь микротрещины. Обе особенности делают первоначальное напряжение-деформацию при нагрузке менее жестким, чем фактическая жесткость породы. После первоначального нагружения порода может показывать линейный отклик — где измеряется модуль Юнга — с последующим разупрочнением, приближающимся к разрушению породы и пиковому напряжению.Когда испытание проводится в неограниченных условиях, пиковое напряжение называется «прочностью на неограниченное сжатие (UCS)» породы (более подробно поясняется в Разделе 4). Коэффициент Пуассона можно измерить в том же диапазоне измерения, в котором доступны датчики поперечной деформации.

Рисунок 3.12: Схема кривой растяжения при одноосном нагружении горных пород в лаборатории.

Модуль Юнга отложений и горных пород варьирует в широких пределах.На рисунке 3.13 показаны типичные значения модуля Юнга.

Рисунок 3.13: Типичные модули Юнга для отложений и горных пород. Значения соответствуют «квазистатическому» нагружению от реакции «напряжение-деформация». СС: песчаник; SiS: Алевролит; Ш: Сланец; Gr: Гранит.

ПРИМЕР 3.2: Вычислить (осевую) деформацию, ожидаемую для породы, подверженной (осевому) напряжению 3000 фунтов на квадратный дюйм при неограниченной осевой нагрузке для:

• Мягкая глинистая порода с E = 1 ГПа
• Песчаник мягкий с E = 10 ГПа.
• Известняк твердый с E = 50 ГПа

РЕШЕНИЕ
Давайте работать в единицах СИ:

psi МПа МПа затем ГПа ГПа ГПа

Обратите внимание, что породы могут быть довольно жесткими, и даже при эффективном напряжении до 3000 фунтов на квадратный дюйм (что эквивалентно глубине на берегу 5000 футов при гидростатическом поровом давлении), деформация приведена в

Введение в материаловедение

Убедитесь, что в вашем браузере включен JavaScript.Если вы оставите отключенным JavaScript, вы получите доступ только к части предоставляемого нами контента. Вот как.

Коллаж из 8 фотографий с текстом «Что общего у всех этих фотографий?» над центром коллажа. На фотографиях по часовой стрелке слева вверху: падающая башня Пизы, безрукая статуя Венеры Милосской, банка с газировкой, которую вот-вот открывают, сломанный карандаш, собака, жующая кость, треснувший Колокол Свободы, Tacoma Narrows Мост, когда его палуба обрушивается, и разбитое лицо и разрушенное тело Сфинкса.

Коллаж, состоящий из 8 изображений, по часовой стрелке от верхнего левого угла: падающая башня Пизы, безрукая статуя Венеры Милосской, банка из-под газировки, которую вот-вот открыли, щелкнувший карандаш, собака, жующая кость, треснувшая свобода Белл, мост через пролив Такома, когда его палуба обрушивается, а также разбитое лицо и разрушенное тело Сфинкса.

Коллаж из 8 фотографий с текстом «Каждая — пример того, как ломается материал!» по центру изображения.На фотографиях по часовой стрелке слева вверху: падающая башня Пизы, безрукая статуя Венеры Милосской, банка с газировкой, которую вот-вот открывают, сломанный карандаш, собака, жующая кость, треснувший Колокол Свободы, Tacoma Narrows Мост, когда его палуба обрушивается, и разбитое лицо и разрушенное тело Сфинкса.

Как вещи ломаются!

Иногда мы хотим, чтобы что-то сломалось. . .

Взлом — не всегда плохо. Например, для банок из-под газировки мы хотим, чтобы ободок вокруг отверстия сломался раньше всего.У вас когда-нибудь отрывался язычок перед открытием банки? Разве вы не ненавидите, когда это происходит? Подумайте о двух разных объяснениях отказа такого вида газированных банок.

Иногда нет!

По очевидным причинам мы хотим, чтобы мосты были прочными и выдерживали множество различных условий окружающей среды.

Для получения дополнительной информации о катастрофе Tacoma Narrows Bridge, эти онлайн-ссылки — хорошее место для начала:

Вопросы

• Как узнать, сломается ли конструкция?
• Из чего состоят разные конструкции и каковы их свойства?
• Какие слова мы используем для описания этих свойств?
• Как мы проверяем эти свойства?

Словарь

Звездная величина

Метрические префиксы
Yotta-	Y	10 24	1 000 000 000 000 000 000 000 000 000
Zetta-	Z	10 21	1 000 000 000 000 000 000 000 000
Exa-	E	10 18	1 000 000 000 000 000 000
Пета-	-П	10 15	1 000 000 000 000 000
Тера-	Т	10 12	1 000 000 000 000
Гига-	G	10 9	1 000 000 000
Мега-	M	10 6	1 000 000
килограмм	к	10 3	1000
га —	ч	10 2	100
дека-	da	10 1	10
–	–	–	–
деци-	д	10 -1	0.1
санти-	с	10 -2	0,01
милли-	м	10 -3	0,001
микро-	мкм	10 -6	0,000 001
нано-	n	10 -9	0,000 000 001
пико-	с.	10 -12	0.000 000 000 001
фемто	f	10 -15	0,000 000 000 000 001
атто-		10 -18	0,000 000 000 000 000 001
zepto-	z	10 -21	0,000 000 000 000 000 000 0001
лет-	y	10 -24	0.000 000 000 000 000 000 000 0001

В США мы используем английскую систему, но все остальные в мире (включая Англию!) Используют метрическую систему. Вы наверняка видели некоторые из этих метрических префиксов раньше, например: милли, метра, гига, байта, нано, секунды.

Для интересного упражнения с величинами вещей попробуйте придумать различные измерения, для которых каждый из вышеуказанных префиксов был бы удобен.Вот несколько ссылок:

Напряжение

Это стресс ??

О чем вы обычно думаете, когда слышите слово «стресс»?

Нет, это стресс!

Диаграмма напряжений при растяжении и сжатии. Напряжение — это сила, действующая на материал, деленная на площадь поперечного сечения материала. Если сила растягивает материал (груз, подвешенный к объекту), это называется растягивающим напряжением.Если сила сжимает материал (груз, помещенный на верхнюю часть объекта), это называется сжимающим напряжением.

С точки зрения материаловедения и машиностроения, напряжение определяется как сила, действующая на материал, деленная на площадь поперечного сечения материала ( A на диаграмме выше). Мы можем говорить о разных типах стресса в зависимости от того, как приложена сила. Например, если сила стремится растянуть материал (как на диаграмме слева), мы называем это растягивающим напряжением .Если сила имеет тенденцию сдавливать материал (как на диаграмме справа), мы называем это напряжением сжатия .

Что происходит, когда вы подвергаете что-то стрессу?

На фото и чертежах деформация показана как изменение длины материала, деленное на исходную длину материала. При растяжении материал может постепенно увеличиваться в длине. При сжатии материал может постепенно уменьшаться в длине.Человек, поднимающий автомобиль, испытывает растягивающее напряжение при вытягивании рук.

Деформация — это реакция материала на напряжение. Он определяется как изменение длины материала, находящегося под напряжением ( L ‘ — L ₀ ), деленное на исходную длину ( L ₀ ). Для материала, находящегося под напряжением, материал может постепенно увеличиваться в длине. Для сжатого материала длина материала может постепенно уменьшаться.

Один из способов продемонстрировать напряжение — использовать сжимаемую упаковочную пену (балки) или изоляцию (трубы). Нарисуйте на поролоне правильную сетку (как показано ниже). Что происходит с шагом сетки, когда вы сжимаете, растягиваете и сгибаете пену? Когда вы изгибаете пенопласт, вы можете увидеть сочетание сжимающих и растягивающих напряжений на противоположных сторонах изгиба.

Механические свойства материалов

Диаграмма описывает модуль упругости и коэффициент Пуассона относительно напряжения и деформации в материале.Модуль упругости равен напряжению, разделенному на деформацию, и обозначается заглавной буквой E. Коэффициент Пуассона равен изменению напряжения вдоль оси x, деленному на изменение напряжения вдоль оси z или изменение напряжения вдоль оси y. делится на изменение напряжения по оси z.

Как инженеры-механики описывают поведение материала при нагрузке? Одно измерение называется модулем упругости и определяется как напряжение, деленное на деформацию.Это мера того, какая деформация создается при данной нагрузке на материал. Другой показатель — это коэффициент Пуассона, который описывает, как напряжение, приложенное вдоль одного измерения материала, влияет на другие измерения.

Вот демонстрация, которую вы можете попробовать сами. В качестве одного из примеров сравните детские роллы и веселых владельцев ранчо. Какая разница? Как каждый реагирует на растягивающие и сжимающие силы? Что с этим произойдет, если сжать зубочистку? Такие материалы, как рулетики, ириска и карамель деформируются пластически (изменяют форму навсегда).Они также становятся намного шире, когда становятся короче, или уже, если растягиваются дольше. Как насчет веселого владельца ранчо? Они хрупкие, поэтому не деформируются пластически до того, как сломаются в результате разрушения. Другие материалы, которые вы можете попробовать, — это глупая замазка (см. Химия слизи для рецепта приготовления самостоятельно) и кубиками льда.

Оборудование для испытаний на растяжение

На фотографии машины для испытания на растяжение показаны чертежи металлического стержня, который помещают в центр машины для проверки ее прочности.Машина имеет две головки, одна подвешенная над другой, которые удерживают материал, в то время как рычаги по бокам машины толкают или стягивают головки вместе для проверки материала. Под фотографией приведены уравнения для напряжения (сила / площадь поперечного сечения) и деформации (изменение длины / исходной длины).

Материаловеды и инженеры-механики используют специализированное испытательное оборудование, такое как машина для испытания на растяжение на диаграмме выше, для измерения реакции материала на нагрузку. Испытательное оборудование может прикладывать большое количество силы.Как величину, так и продолжительность действия силы можно точно измерить. На диаграмме также показаны типичные характеристики пластичных материалов при растяжении.

Как нетрудно догадаться, такое специализированное испытательное оборудование стоит дорого. Есть гораздо более дешевые методы, которые вы можете использовать для измерения стресса и напряжения для своего научного проекта. Например, см. Сила в цифрах?

Зачем тестировать материалы?

Хорошие вопросы:

• Как мы выбираем материалы?
• Как убедиться, что то, что мы делаем, хорошо?
• Как убедиться, что он безопасен, когда мы его построим?
• Как сделать так, чтобы это продолжалось?

Это некоторые из многих веских причин для тщательного тестирования материалов.

• Исследования. Нам нужны точные измерения свойств существующих материалов, чтобы инженеры могли выбрать правильный материал для конкретного проекта. Материаловедам, разрабатывающим новые материалы, нужны способы измерения прогресса.
• Контроль качества при производстве. Тестирование гарантирует, что производственный процесс работает должным образом. Когда материалы не проходят проверку качества, причину дефекта (-ов) можно отследить, а проблему на производственной линии можно устранить.
• Характеристики зданий / устройств в заводском состоянии. Когда инженеры проектируют продукт, они ожидают, как его конструкция будет работать (на основе моделей и прототипов, известных свойств материалов и опыта). Взяв реальный продукт, только что сошедший с конвейера, и протестировав его, мы можем измерить, насколько дизайн выдерживает реальный мир.
• Тестирование жизненного цикла. Автоматическое тестирование с повторяющимися циклами нагрузки может дать информацию о том, как долго материалы могут прослужить в различных условиях окружающей среды.

Результаты испытаний на растяжение

График напряжения-деформации для пластичных материалов

Примерный график зависимости напряжения от деформации показывает приложенное напряжение и измеренную деформацию в пластичном материале до разрушения материала. Пластичный материал — это материал, который перед разрушением может сгибаться или сгибаться. График показывает неуклонное увеличение напряжения и деформации перед небольшим провалом, при котором материал больше не может изгибаться и внутри материала начинает расти напряжение.Напряжение продолжает медленно увеличиваться, пока не достигает пика, и медленно уменьшается, в то время как напряжение постоянно нарастает. В конце концов напряжение и напряжение становятся слишком большими, и объект разрывается или ломается. Напряжение, измеренное в точке разрыва, является точкой напряжения разрушения.

Вот пример того, как специалисты по обработке данных используют при оценке пластичных материалов. Приложенное напряжение откладывается по оси y, а измеренная деформация в ответ на это напряжение откладывается по оси x.Приведенные ниже определения помогут вам понять схему.

• Материал, который может подвергаться большой пластической деформации до разрушения, называется пластичным материалом .
• Материал, который демонстрирует небольшую пластическую деформацию при разрушении или не проявляет ее вовсе, называется хрупким материалом .
• Точка, до которой напряжение и деформация линейно связаны, называется пределом пропорциональности .
• Наибольшее напряжение на кривой «напряжение-деформация» называется пределом прочности .
• Напряжение в точке разрыва называется напряжением разрыва или разрывом напряжения.
• Область кривой «напряжение-деформация», в которой материал возвращается к недеформированному напряжению при снятии приложенных сил, называется упругой областью .
• Область, в которой материал постоянно деформируется, называется пластической областью .
• Точка, отделяющая эластичный элемент от области пластика, называется пределом текучести .Напряжение в пределе текучести называется пределом текучести .
• Остаточная деформация при нулевых напряжениях называется пластической деформацией .
• Напряжение текучести — это напряжение, которое вызовет пластическую деформацию, соответствующую заданной деформации смещения .
• Твердость — сопротивление вдавливанию.
• Повышение предела текучести с увеличением деформации называется деформационным упрочнением .
• Внезапное увеличение площади поперечного сечения после предельного напряжения называется сужением . На рисунке ниже показан пример сужения.

Моменты и моменты

Моменты и крутящие моменты на инженерном языке означают напряжения, которые мы обычно называем «изгибом» и «скручиванием». Это все те же идеи напряжения и напряжения, о которых мы говорили, и те же единицы измерения. Разница в оси приложения напряжения.

На диаграмме видно, что моменты создают как сжимающие (−σ), так и растягивающие (+ σ) напряжения, в зависимости от того, какую часть материала вы исследуете. Вы можете использовать балки и трубы из пенопласта с сеткой (из сжимаемого пенопласта и изоляции труб соответственно), чтобы визуализировать влияние моментов и крутящих моментов. Проведите линии сетки через 2-3 интервала.

Пластичный или хрупкий?

Материалы с разными свойствами ломаются по-разному.Вспомните веселых владельцев ранчо и сладких булочек. Какой пластичный, а какой хрупкий? Подумайте о скрепке. Пластичный или хрупкий? Вы можете использовать его на небольшой стопке бумаги много раз, и она вернется к своей первоначальной форме. Но если вы откроете скрепку, как показано выше, вы деформируете ее пластически, и она навсегда сохранит новую форму после превышения предела текучести. Как насчет лобового стекла?

Как вещи ломаются?

Коррозия

Металлы прочные, но они подвержены коррозии или ржавчине.Краска помогает защитить металл от воды и воздуха, которые являются ингредиентами коррозии.

Усталость

Повторяющаяся нагрузка открывает и закрывает крошечные дефекты снова и снова, и в конечном итоге эти дефекты превращаются в трещины, которые распространяются и разрушаются. При повторяющейся нагрузке конструкции в конечном итоге разрушаются при гораздо меньших нагрузках, чем предполагалось изначально. Возьмите скрепку и попробуйте развернуть и сложить ее в разных направлениях (вращая или сгибая).Попробуйте ездить на велосипеде с разными диапазонами отклонения и подсчитайте количество циклов, необходимых для разрыва скрепки. Есть ли связь между углом отклонения и количеством циклов до поломки?

Пластиковый человек или Человек из стали?

Пластмассы дешевы, им легко придать форму, они легкие и довольно прочные для своего веса, но они легко размягчаются при температуре. Их соотношение прочности к весу не так хорошо, как у стали, популярного конструкционного материала.Однако сталь довольно тяжелая и подвержена коррозии.

А как насчет этих материалов?

Керамика хрупкая, алюминий пластичный. Бетон обычно армируют внутри металлическими прутьями, поэтому вся конструкция имеет смешанные свойства.

Объединение материалов

Насколько прочны разные конструкции? Какие преимущества у разных форм?

Прочность зависит от:

• Свойства материала
• Геометрия (e.г., форма поперечного сечения материала)
• Характер и размещение опоры

Чем материалы на иллюстрации выше отличаются по свойствам материала, геометрии и размещению опоры?

А как насчет этих структур?

Эти продукты были разработаны с использованием композитов из углеродного волокна, чтобы быть легкими, но очень прочными. Как свойства материала, геометрия и размещение опор придают каждому изделию прочность?

Для проектов, которые исследуют силу vs.геометрию см .:

Делаем вещи прочными и легкими

Как сделать вещи прочными и легкими?

• Геометрия: умные формы выдерживают большие нагрузки.
• Материалы: выбор подходящего материала для работы.

Требуется сочетание качественных материалов и правильной формы.

Отношение прочности к массе

Как мы можем измерить, чтобы увидеть, что работает лучше всего?

• Мы можем сравнивать различные конструкции и материалы, сравнивая соотношение прочности к весу каждой из них с другими.
• Возьмем прочность материала (сила или разрывное напряжение) и разделим на его вес , чтобы получить отношение прочности к весу.

Сильный и легкий: галерея изображений

Геометрия — Здания

Эта галерея изображений может вдохновить вас на создание прочных и легких конструкций. Информацию о проекте, в котором вы можете применить эти идеи, см. Падающая башня макаронных изделий.

Здание банка Гонконга и Шанхая имеет треугольные рамы вокруг высоких стержней, чтобы стержни могли поддерживать здание и не прогибались.Архитекторы часто играют с геометрией при проектировании зданий. Использование простых форм помогает снизить стоимость и вес материала, сохраняя при этом безопасность и поддержку здания.
Эйфелева башня достигает большой коэффициент прочности к массе за счет использовани фермы опорной конструкции.
Строительный кран — это высокая башня с ферменной рамой, предназначенная для подъема и перемещения тяжелых предметов. Высота конструкции по сравнению с ее весом очень хороша по сравнению с тем, какой вес она может поднять.

Конструкционные пластмассы

Различные материалы обладают разными свойствами. Многие металлы, например сталь, очень прочные, но при этом очень тяжелые. Конструкционные твердые пластмассы прочные и долговечные, им можно придать практически любую форму и они легкие.

Канаты и шнуры

Даже простые вещи, такие как веревки и шнуры, могут обладать огромной прочностью для своего веса.Они используют тот факт, что материалы, из которых они сделаны, очень прочны на растяжение.

Superstrong: материалы и геометрия

Углеродное волокно — еще один материал, устойчивый к растяжению. Если скомбинировать его с сотовой формой, которая хорошо поддается сжатию, получается очень прочная структура.

Как материалы (например, полая рама из титана или углеродного волокна), так и геометрическая треугольная форма велосипеда позволяют ему быть очень прочным при небольшом весе.

Природные материалы

Паучий шелк обладает удивительными свойствами.

• На ощупь он похож на шелк и эластичен, как нейлон.
• Он в 3 раза легче кевлара (самого прочного искусственного волокна, используемого в пуленепробиваемых жилетах) и до 30 раз прочнее!
• Если бы волокна паучьего шелка были созданы диаметром с маленький карандаш и скручены в паутину, они смогли бы остановить реактивный самолет Боинг 747 в воздухе (как вы видите в «Человеке-пауке»)!

Многие материалы, встречающиеся в природе, обладают очень интересными свойствами, которые люди не могут скопировать.

Древесина имеет высокое отношение прочности к массе благодаря своей ячеистой микроструктуре. То, как растут клетки дерева (в зернах), делает древесину прочной.

Даже разные породы дерева обладают разными свойствами. Например, древесина бальзы чрезвычайно легкая, но при формовании правильной формы она также чрезвычайно прочна. Эта конструкция из пробкового дерева и суперклея весила всего 18 грамм, но выдержала 990 кг перед тем, как сломаться !!

Фотографии моста из бамбука и бамбука, растущего в природе.Стебель бамбукового растения называется стеблем, он легкий и прочный из-за стеновых перегородок, которые проходят и укрепляют весь стебель. Бамбук также быстро растет, его можно найти разных форм и размеров, он отлично подходит для строительства зданий, мостов и инструментов.

Бамбук — еще один природный ресурс для изготовления строительных материалов.

Страницы «Напряжение, напряжение и сила» были адаптированы из программы семинаров, разработанной в Стэнфордском университете для учащихся 7-х классов, интересующихся инженерными науками.Первокурсники Стэнфордского университета были наставниками программ. Мастерская разработана:

Профессор Бет Прюитт, машиностроение, Стэнфордский университет.
Тори Бейли, доктор философии. Кандидат технических наук, Стэнфордский университет
Алекс Тунг, Ph.D. Кандидат электротехники, Стэнфордский университет

Разработчики дали разрешение на публикацию этих материалов на сайте Science Buddies.

Отредактировал Эндрю Олсон, доктор философии, приятели науки.

Видео о нашей науке

10 проектов робототехники, которые действительно могут осуществить дети!

Почему яблоки и бананы коричневеют? — STEM-деятельность

4 простых проекта по науке о роботах для детей

«Напряжение, деформация и свойства материалов», EPI Inc.

Краткий обзор основ

ПРИМЕЧАНИЕ: Все наши продукты, конструкции и услуги ЯВЛЯЮТСЯ ОРГАНИЧЕСКИМИ, БЕЗ ГЛЮТЕНА, НЕ СОДЕРЖАТ ГМО и не нарушат чьи-либо драгоценные ЧУВСТВА

Чтобы лучше понять различные дискуссии о нагрузках, напряжениях и ожидаемом сроке службы компонентов, полезно понять основные термины, используемые в этих обсуждениях. В следующих параграфах дается очень краткое описание этих терминов.Обратите внимание, что это очень простое объяснение предметов, которые некоторые инженеры изучают на протяжении всей своей карьеры.

НАПРЯЖЕНИЕ НА РАСТЯЖЕНИЕ И СЖАТИЕ

Напряжение — это величина, которая описывает величину нагрузки, которую несет каждая единица площади поперечного сечения компонента. Например, предположим, что блок, показанный на Рисунке 1, весит 10500 фунтов и подвешен на валу (с наконечником стрелки). Диаметр вала составляет 0,504 дюйма, поэтому его площадь поперечного сечения составляет 0,200 квадратных дюймов (дюйм²).

Рисунок 1

Напряжение, прилагаемое к валу нагрузкой 10 500 фунтов, определяется как нагрузка, деленная на площадь поперечного сечения вала , которая составляет 10 500 фунтов ÷ 0,200 квадратных дюймов = 52 500 фунтов на квадратный дюйм (psi). Обратите внимание, что эта «нагрузка на единицу площади» является концепцией ДАВЛЕНИЯ, представленной в параметрах «Сила, давление и трение».

Если диаметр вала увеличить до 3/4 дюйма, площадь увеличится до 0,4418 квадратных дюймов (дюйм²), а напряжение уменьшится до 10 500 ÷ 0.4418 = 23 766 фунтов на квадратный дюйм.

Поскольку нагрузка, показанная на рисунке, пытается удлинить вал, это называется напряжением растяжения . Если перевернуть изображение так, чтобы вал поддерживал блок снизу, блок будет пытаться укоротить вал, и напряжение будет называться сжимающим напряжением и напряжением .

Нагрузки, которые создают растягивающие и сжимающие напряжения, действуют перпендикулярно областям, на которые они действуют. Растягивающие и сжимающие напряжения часто называют нормальными напряжениями.Здесь «нормальный» — это не поведенческий термин, а геометрический, который в данном контексте означает «, действующий перпендикулярно » определенной области или плоскости.

НАПРЯЖЕНИЕ НА СДВИГ

Рисунок 2

Силы, действующие параллельно областям сопротивления, известны как силы сдвига, и создают напряжение сдвига в элементах, которые несут эти нагрузки.

Например, предположим, что две вилки (вилки?) На этом рисунке имеют равные растягивающие силы, действующие на их концы («перпендикулярно» торцам), как показано стрелками.Эти силы пытаются развести вилки друг от друга, и при этом они прикладывают силу сдвига (параллельную площади поперечного сечения болта) к болту, удерживающему детали вместе. Сила сдвига пытается разрезать болт пополам по его диаметру в двух местах, где две внешние поверхности нижней вилки встречаются с двумя внутренними гранями верхней вилки. Этот случай известен как «двойной сдвиг», потому что есть две отдельные области болта, подверженные действию силы сдвига.

Предположим, что болт в этом примере имеет диаметр 3/4 дюйма, а обе растягивающие нагрузки составляют 20 000 фунтов.Площадь поперечного сечения болта составляет 0,4418 квадратных дюймов (дюйм²). Тогда напряжение сдвига, приложенное к болту, будет составлять 20 000 фунтов, разделенных на удвоенную площадь болта (поскольку нагрузка распределяется на две различные площади поперечного сечения болта), или 22 634 фунта на квадратный дюйм.

Важно отметить, что способность большинства металлических материалов выдерживать напряжение сдвига значительно меньше их прочности на растяжение или сжатие.

НАПРЯЖЕНИЕ ИЗГИБА

Рисунок 3

Напряжение изгиба возникает, когда компонент нагружается силами, которые вместо того, чтобы пытаться растянуть или сжать компонент, пытаются согнуть его на .Эти изгибающие силы создают комбинацию растягивающего и сжимающего напряжения в несущих компонентах, известную как изгибающее напряжение .

Пример такого типа нагрузки показан на tРисунке 3, где трубчатый вал опирается на две треугольные опоры. Две вертикальные стрелки представляют собой направленные вниз силы, приложенные к трубке. Трубка отклоняется или изгибается вниз под действием этих сил, как показано на рисунке.

Если вы прорежете секцию трубы у правой опоры и сможете визуализировать внутренние напряжения между молекулами металла на поверхности разреза, они появятся как напряжения растяжения и сжатия, показанные зелеными стрелками на рисунке 4.Величина напряжения наибольшая на внешних концах и уменьшается до нуля в геометрическом центре.

Рисунок 4

Напряжение изгиба рассчитывается на основе свойств поперечного сечения и величины изгибающего момента . Изгибающий момент равен величине приложенной силы, умноженной на расстояние от точки приложения силы до исследуемого поперечного сечения. Это горизонтальное расстояние от точки приложения силы (фиолетовая стрелка) до поперечного сечения называется плечом момента.(Это значительное упрощение, но оно иллюстрирует концепцию.)

ШТАМ

Деформация — это мера степени деформации материала при приложении к нему нагрузки, выраженная в дюймах деформации на дюйм длины материала. Например, если вал диаметром 1/2 дюйма, поддерживающий нагрузку в 10 000 фунтов на Рисунке 1, имеет длину 12 дюймов, он будет растягиваться примерно на 0,020 дюйма (20 тысячных) от своей длины без нагрузки, которую вы можете измерить. Деформация — это измеренное отклонение (0,020) деленное на длину вала, или 0.020 ÷ 12 = 0,00167 дюйма на дюйм.

Предположим, вы измеряете образец, к которому не приложена нагрузка. Затем вы прикладываете нагрузку к образцу, затем снимаете нагрузку и снова измеряете образец. Если вы обнаружите, что он вернулся к своей исходной длине, значит, образец испытал упругую деформацию при растяжении под нагрузкой.

Большинство материалов — это эластичный . То есть, если вы приложите к материалу нагрузку, он каким-то образом деформируется на величину, пропорциональную нагрузке.Когда вы снимаете нагрузку, материал вернется к своей исходной форме, если нагрузка не будет слишком большой. Деформация может быть слишком мала для измерения, но она все равно возникает.

Если после снятия нагрузки вы можете измерить некоторую остаточную деформацию в образце (образец не возвращается к своей исходной длине), значит, материал подвергся напряжению, превышающему предел упругости и испытал пластик деформация.

НАПРЯЖЕНИЕ ДОПУСТИМОСТИ и ПРЕДЕЛЬНОЕ НАПРЯЖЕНИЕ

Есть два основных значения, характеризующих прочность металла. Каждое из этих значений представляет собой уровень напряжения , при котором происходит конкретное событие.

Рисунок 5

Темная линия на рисунке 5 показывает растяжение образца в ответ на приложенное растягивающее напряжение. В этом примере от 0 до 70 000 фунтов на квадратный дюйм растяжение (деформация) пропорционально напряжению, и если нагрузка снимается, образец возвращается к своей исходной длине.Это известно как упругая деформация .

Однако, если нагрузка (в этом примере) превышает 70 000 фунтов на квадратный дюйм, обратите внимание, что деформация становится больше на единицу увеличения напряжения и больше не пропорциональна напряжению. После того, как этот образец был нагружен свыше 70 000 фунтов на квадратный дюйм, образец не возвращается к своей исходной длине (красная линия) при снятии нагрузки. Образец деформирован остаточно ( пластическая деформация ).

Уровень напряжения, при котором материал больше не ведет себя упруго, а вместо этого испытывает небольшую остаточную (пластическую) деформацию, известен как предел текучести (YS) (также известный как предел пропорциональности ) .Это уровень напряжения, при котором был превышен предел упругости материала.

Второе интересное значение называется предельным напряжением при растяжении (UTS). Это значение напряжения, при котором материал разрушается под действием чистого растягивающего напряжения.

Для измерения этих значений используется специализированная испытательная машина. Небольшой образец исследуемого металла (обычно диаметром 0,357 дюйма или 0,504 дюйма) устанавливается в машину, как показано на рисунках 6 и 7 ниже.

Рисунок 6

Рисунок 7

Машина прикладывает растягивающую нагрузку к образцу и увеличивает нагрузку до тех пор, пока образец не сломается.Компьютер, который управляет машиной, строит график зависимости нагрузки от прогиба в реальном времени и определяет предел текучести . В какой-то момент после того, как материал начинает уступать, оператор приостанавливает испытание и снимает датчик отклонения (чтобы предотвратить его разрушение при разрушении образца). Затем оператор возобновляет испытание, и машина продолжает увеличивать нагрузку до тех пор, пока образец не сломается. Нагрузка, при которой образец сломался, делится на исходную площадь поперечного сечения (0.100 дюймов² для диаметра 0,357 дюйма или 0.200 дюймов² для диаметра 0,504 дюйма), чтобы найти значение UTS. Когда образец приближается к точке разрушения, часть диаметра (где произойдет разрушение) начинает пластически деформироваться и уменьшаться в диаметре («сужение»). Процент, на который уменьшается площадь поперечного сечения материала, является мерой пластичности (отсутствия хрупкости) материала и выражается как процент уменьшения площади (ROA).

КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЯ

Уже давно известно, что наличие неровностей или неоднородностей в детали (отверстия, резкие изменения диаметра, выступы, канавки, выемки и т. Д.)) значительно увеличивает значение фактического напряжения , которое возникает в детали, по сравнению со значением напряжения , рассчитанным для на основе поперечного сечения детали. Это увеличение напряжения, называемое концентрацией напряжения , происходит в непосредственной близости от неоднородности.

Отношение фактического напряжения к расчетному напряжению известно как коэффициент концентрации напряжений . Величина коэффициентов концентрации напряжений может составлять 3, 4 или более в зависимости от серьезности конкретного нарушения сплошности.

Это явление можно продемонстрировать на тестах. Накоплен большой объем данных, связывающих физические характеристики неоднородностей различных типов с увеличением наблюдаемого напряжения, которое они вызывают. Есть несколько книг, в которых представлены методы расчета этих факторов. Одна из наиболее популярных работ по этой теме — «Факторы концентрации стресса» Петерсона ( ref-2: 4 ). Некоторые системы FEA учли эффект разрывов в своих расчетах.

Существует также несколько общепринятых методов уменьшения эффекта неоднородностей, повышающих напряжение, включая конусность, большие радиусы скругления, закругленные поднутрения и пологие неоднородности, окружающие обязательно резкую.

В качестве примера методов тезисов, рассмотрят рисунок ниже, показывающая типичный входной вал для автомобильной трансмиссии, с плечом для опорного подшипника и оснастка кольца удерживающего подшипника на плече.

Следующие две фотографии показывают поперечное сечение вала, изображенные выше, без подшипника или оснастки установлено кольцо.На рисунке 8 показан типичных реализации вала, с острой треугольной канавкой под стопорным кольцом (необходимо очистить края стопорного кольца), и остроугольным плечом, требуется, чтобы очистить малый радиус на кромке подшипника, как правило, меньше, более 0,040 дюйма. Острые углы в канавке и заплечике обеспечивают высокую концентрацию (до 10: 1) приложенных напряжений, заставляя материал вести себя в условиях усталости (следующая тема), как если бы приложенное напряжение было значительно большим. Сравните вал на рисунке 8 к лучшей конфигурации, показанной на рисунке 9, который имеет каплевидную, большого радиуса канавки на обеих сторонах остроугольное канавкой под стопорное кольцо, и который имеет большой радиус выточку в плечо подшипника.Эти положения резко снижают концентрацию напряжений (до 1,5: 1) по сравнению с рисунком 8.

Рисунок 8

Рисунок 9

.